Математика в строении зданий

От чего же ещё зависит прочность сооружений? От конструкции, которая используется как основа при его проектировании и строительстве. Если связывать прочность с материалами, из которых они созданы, с особенностями конструктивных решений, то выявляется, что прочность сооружений зависит ещё и от той геометрической формы, которая является базовой. Мы говорим сейчас о том, что архитектурное сооружение можно представить, как помещённое в определённое геометрическое тело, причём, как можно ближе к его границам. Т.е. другими словами, любое сооружение можно образно вписать в какое либо тело (геометрическое, конечно), которое может рассматриваться, как модель этой архитектурной формы. Самыми прочными сооружениями с давних времён считаются Египетские пирамиды.

Они имеют форму четырёхугольных пирамид (иногда ступенчатую или башнеобразную), в основании которых четырёхугольник, а остальные грани - треугольники, имеющие общую вершину. Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счёт большой площади основания.

На смену пирамидам пришла стоечно-балочная система. Она состоит из двух вертикально стоящих прямоугольных параллелепипеда, на которые сверху ставится ещё один прямоугольный параллелепипед.

Первым таким сооружением был – Дольмен, это мегалитическое сооружение в виде большого каменного ящика, накрытого плоского плитой. Также до нас дошло ещё одно сооружение, представляющее простейшую стоечно-балочную конструкцию – Кромлех. Это тоже мегалитическое сооружение, но уже эпохи неолита и бронзового века, в виде круговой ограды из огромных камней, предназначенное для жертвоприношений и ритуальных тождеств.

Большинство современных жилых домов имеют в своей основе стоечно-балочную конструкцию, что говорит о наибольшей распространённости этой системы в строительстве и в наши дни.

Прочность архитектурных сооружений – важнейшее их качество, но нельзя забывать и о, удобстве этих сооружений, которое всегда должно присутствовать. Обратимся к жилым зданиям. Ведь именно квартира, дом должны быть, прежде всего, удобными, т.к. именно в них мы проводим большую часть своей жизни. Как всем известно, архитектор делает архитектурные чертежи зданий, квартир, сооружений, чтобы всё рассчитать и потом по ним строить.

Вспомним архитектурные чертежи недавнего прошлого (XVI-XVII веков), которые делались вне правил начертательной геометрии, архитектор решал стоящие перед ним задачи, совмещая планы с фасадами.. Теперь же современный нам архитектор, проектируя, чертит строго в ортогональных проекциях. На этих чертежах решаются задачи соразмерности и пропорциональности. На их основе осуществляется строительство. Перспективный вид и даже модель здания не могут заменить такой чертёж.  

Математика в планировании помещений

Как же математика может помочь в планировании помещений? Во-первых, при составлении плана чаще всего решается геометрическая задача о разбиении многоугольника на части. Во-вторых, архитектор обязательно пользуется понятием масштаб, т.к. все размеры реальных помещений он уменьшает в какое-либо одинаковое количество раз. Он изображает план с точки зрения геометрии, представляя его в виде той фигуры, которую можно было бы увидеть, смотря на неё сверху. Далее математика помогает архитектору сделать соответствующие расчёты по известным ему специальным формулам, чтобы решить какой толщины должны быть стены и сколько слоёв звукоизолирующего материала необходимо проложить, чтобы обеспечит жильцам комфортные условия жизни.

Сооружения могут быть прочными и удобными, но если они не привлекают взгляд, то они уже воспринимаются, как обычные строения, но не как памятник архитектуры. Опять же, какое-либо сооружение может стать не прочным и следовательно совсем неудобным и бесполезным, но если оно красиво и вызывает чувство восторга, то при этом его архитектурная ценность не исчезнет. Снова приведём пример на Преображенском соборе на острове Кижи. Ведь он был построен, как уже говорилось, полностью из дерева и со временем стал разрушаться, из-за чего его перестали использовать по назначению, но однако же он не перестал быть шедевром искусства. И так произошло со многими сооружениями древнерусского зодчества. Также можно привести ещё один явный пример – «падающая» башня в Пизе.

«Падающая башня». Колокольня Пизанского собора. Высота сооружения 55м. Начала строиться в 1179 году рядом с собором. Башня стала отклоняться ото вертикали уже в процессе постройки. В конце 1990-х гг. реставрационные работы, с помощью которых башня стала «скользить» в обратном направлении.

Зададимся вопросом: «А что же архитектуру делает красивой, из-за чего она становится ценной?» Существуют конкретные математические модели, соотношения и свойства, разнообразные геометрические формы, пропорции и законы симметрии (о которых подробно говорить мы будем позже), которые в определённой мере задают внутреннюю красоту архитектурной формы.

Математика предлагает архитектору, как бы общие правила, основы организации частей в целое, которые помогают расположить эти части в пространстве, установить соотношение между размерами частей, выделить определённое место опять же в пространстве, где будет располагаться сооружение, описать его определённой математической формой, которая позволит выделить его из других сооружений и внести в их состав, создав новую композицию.

Форма, в основе построения которой лежат сочетания симметрии и золотого сечения, способствуют наилучшему восприятию и проявлению ощущения красоты и гармонии. Гармонические особенности произведения нельзя рассматривать в отрыве от идеи произведения, однако они коренятся в какой-то мере и в физиологических особенностях человеческого восприятия. Математическая характеристика физиологического механизма (органов чувств) является подосновой гармонизации формы в архитектуре.

Также в основе нашего восприятия лежит принцип геометрического подобия. Этот же самый принцип позволяет нам использовать природные формы, их комбинации в архитектурных сооружениях, внося в них природную красоту. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Итак, в архитектуре существуют три основных критерия, которые нужно обязательно учитывать и к которым нужно стремиться, это прочность, удобство, красота.. И добиваться структурного, функционального и видимого совершенства нам помогает именно математика, её закономерности, пропорции, принципы. Даже если подойти с самой простейшей стороны к архитектурным сооружениям, не углубляясь в подробное исследование значения математики в архитектуре, то мы видим, что она везде присутствуют. Её геометрические формы, фигуры лежат в основе любого здания, этого просто не избежать. Даже чтобы узнать ширину или высоту, длину или объём какого-либо предмета, мы наблюдаем чистейшую основу математику, ведь все размеры, это те же самые числа, которые непосредственно относятся к первоначальным ступеням математики. Ни один вид искусств так тесно не связан с геометрией, как архитектура.

Большой вклад внёс знаменитый архитектурный реформатор Ле Корбюзье. Он восторгался «Окружающий нас мир – это мир геометрии чистой, истинной, безупречной в наших глазах. Всё вокруг – геометрия». Ле Корбюзье считал геометрию тем замечательным инструментом, который позволяет установить порядок в пространстве. Все архитектурные произведения живут в пространстве, являются его частью, вписываясь в определённые геометрические формы. Каждое единое целое состоит из отдельных частей, деталей, каждая из которых также строится на базе определённого геометрического тела. Очень часто для разнообразия и определённой красоты геометрические формы являются комбинациями различных геометрических тел. В современной архитектуре, благодаря возможностям современных материалов, архитекторы используют причудливые формы, которые воспринимаются нами через их сложные, изогнутые (выпуклые и вогнутые) поверхности.

Математика, геометрия являются "оформлением" строительной деятельности, без которых она просто невозможна. Недаром геометрия оказалась впереди других наук и вооружила человека в его строительной, как, впрочем, и во всякой иной созидательной деятельности.
 Геометрия помогает не просто строить, она, выполняя технические функции, одновременно гармонизирует форму и, более того,служит одним из важных средств образной характеристики произведений архитектуры.

Из многих отношений, которыми издавна пользовался человек при создании гармонических произведений, существует одно, единственное и неповторимое, обладающее уникальными свойствами. Оно отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по-разному – «золотой», «божественной». Древнейшие сведения о ней относятся ко времени расцвета античной культуры. 

Принципы золотого сечения используются в архитектуре и в изобразительных искусствах. Термин «золотое сечение» ввел Леонардо да Винчи.

Теперь для полной убедительности и понимания ценности и значения отношения золотого сечения, рассмотрим пропорциональность пирамид Хеопса и Хефрена, где наиболее явно используется этот принцип, т.е. принцип золотого сечения. Нет сомнений в том, что, предпринимая строительство таких гигантов, зодчие очень и очень внимательно рассчитывали все их размеры. Иначе невозможно мыслить организацию этого чрезвычайного по масштабам строительства. Точные соразмерности этих сооружений не вызывают ни малейших сомнений.

Пирамида Хеопса имеет стороны основания: 230,41, 230,51, 230,60 и 230,54м. Высота равна 146,70 м. Отношение наклонной образующей, или гипотенузы прямоугольного треугольника, образующего поперечный разрез пирамиды к малому катету, или половине стороны квадратного основания, равно отношению золотого сечения.

Пирамида Хефрена построена на основе отношений сторон священного египетского треугольника. Ее поперечный разрез определяется двумя треугольниками, сблокированными своими большими катетами. Проверим. Сторона основания равна 215,86м, высота равна 143,65м. Архитектурные формы пирамиды Хефрена как нельзя лучше свидетельствуют об использовании, зодчими Египта целочисленного треугольника 3, 4, 5.
 Анализ пропорций пирамид не оставляет и тени сомнения в том, что зодчие древнего Египта превосходно знали и высоко ценили отношение золотого сечения.

Информационный бум

Сейчас много говорят об информационном буме. Поток информации захлестывает: утверждают, что ее количество удваивается каждые десять лет. Изобразим этот процесс наглядно, в виде графика некоторой функции. Примем объем информации в некоторый год за единицу. Поскольку эта величина послужит нам началом дальнейших построений, отложим ее над началом координат, в которых будет строиться график, по вертикальной оси. Отрезок, вдвое больший, восставим над единичной отметкой горизонтальной оси, считая, что эта отметка соответствует первому десятку лет. Еще вдвое больший отрезок восставим над точкой «два», соответствующей второму десятку, еще вдвое больший — над точкой «три». Декада за декадой— избранные нами значения аргумента выстроятся по горизонтальной оси в порядке равномерного нарастания, по закону арифметической прогрессии: один, два,  три,   четыре...   Значения функции отложатся над ними, возрастая каждый раз вдвое,— по закону геометрической прогрессии: два, четыре, восемь, шестнадцать...

А что если посмотреть, как нарастал поток информации до того года, который принят за начальный? Столь же равномерно, откладывая единицу за единицей, пройдемся по оси абсцисс влево от начала координат и над отложенными значениями аргумента, будем наносить на график значения функции уже в порядке убывания — вдвое с каждым шагом.  Теперь соединим все нанесенные точки непрерывной гладкой линией — ведь количество информации нарастает от десятилетия к десятилетию плавно, а не скачками.  Перед нами график так называемой показательной функции.

Звездный график

Сколько звезд на небе?  Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны, они, как люди, рождаются и умирают. И чтобы будущие исследователи могли следить за возникновением и угасанием звезд, Гиппарх составил свой звездный каталог. Он насчитал около тысячи звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппарх назвал звездами первой величины, заметно менее яркие — второй, еще столь же менее яркие — третьей и так далее в порядке равномерного убывания видимого блеска — до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина.

Когда ученые получили в свое распоряжение чувствительные приборы для световых измерений, стало возможным точно определять блеск звезд. Стало возможным сравнить, насколько соответствует данным таких измерений традиционное распределение звезд по видимому блеску, произведенное на глаз. Оценки того и другого рода сведем на одном графике. От каждой из шести групп, на которые звезды распределил   Гиппарх, возьмем по одному типичному представителю. По вертикальной оси будем откладывать блеск звезды в единицах Гиппарха, то есть ее звездную величину, по горизонтальной — показания приборов. За масштабную единицу горизонтальной оси примем блеск звезды «б Тельца», стоящей посредине в ряду представителей звездного солнца. Отметки на горизонтальной оси располагаются неравномерно. Объективные (прибор) и субъективные (глаз) характеристики блеска не пропорциональны друг другу.

С каждым шагом по шкале звездных величин прибор регистрирует возрастание блеска не на одну и ту же величину, как могло бы показаться, а примерно в два с половиной раза. Образно говоря, глаз сравнивает источники света по блеску, задаваясь вопросом «во сколько раз?», а не вопросом «на сколько?». Мы отмечаем не абсолютный, а относительный прирост блеска. И когда нам кажется, что он возрастает или убывает равномерно, в действительности мы шагаем по его шкале все более размашистыми шагами, покрывая при этом поистине гигантский диапазон: в миллион миллионов раз различаются по блеску источники света, самый слабый и самый мощный, воспринимаемые человеческим глазом.

Именно в силу описанной физиологической особенности звезды, ярко горящие на ночном небе, не видны днем, тонут в ослепительном блеске солнца, рассеянном по небосводу. И там и здесь сияние звезд дает одну и ту же добавку к свету фона. Однако в первом случае (ночью) эта добавка велика по сравнению с мерцанием неба, во втором же (днем) составляет весьма незначительную долю от солнечного блеска (менее чем миллиардную даже для самых ярких звезд). Оттого же и голос солиста, когда его пение подхватывает хор, тонет в многоголосом звучании. Суть функциональной зависимости, описанной нами на примере зрения и слуха, в том, что возрастанию аргумента в одно и то же число раз всегда соответствует оно и то же приращение функции. Когда аргумент меняется по закону геометрической прогрессии, функция меняется по закону арифметической прогрессии.

Как же называется функция, с которой мы познакомились по звездному небу? Ординаты выделенных точек графика являются логарифмами абсцисс, взятых по основанию 2,5. Такую функцию называют логарифмической.
 

Математические портреты пословиц

Современная математика знает множество функций, и у каждой свой неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на Земле. Однако при всей непохожести одного человека на другого у каждого есть руки   и голова, уши и рот. Точно так же облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций.

Функции — это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций, нам показалось естественным обратиться к пословицам. Ведь пословицы — это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа.

«Выше меры конь не скачет» Если представить траекторию скачущего коня как график некоторой функции, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой». Это будет знакомый график функции синуса.

Пересев хуже недосева» Урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга. Эта закономерность станет особенно наглядной, если изобразить ее графиком, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум— это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни.

«Чем дальше в лес, тем больше дров» Можно изобразить графиком, как нарастает количество дров по мере продвижения в глубь леса – от опушки, где все давным-давно собрано, до чащоб, куда не ступала нога заготовителя. График представляет количество дров как функцию пути. Согласно пословице эта функция неизменно возрастает. Такое свойство функции называется монотонным возрастанием.

«Каши маслом не испортишь»  Качество каши можно рассматривать как функцию количества масла в ней. Согласно пословице эта функция не уменьшается с добавкой масла. Она, возможно, увеличивается, но может оставаться и на прежнем уровне. Подобного рода функция называется монотонно неубывающей.

Биография.

Николай Иванович Лобачевский — российский математик, один из создателей неевклидовой геометрии, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд  назвал Лобачевского «Коперником геометрии».

Рисунок 1. Н.И. Лобачевский

Лобачевский в течение 40 лет преподавал в Императорском Казанском университете, в том числе 19 лет руководил им в должности ректора; его активность и умелое руководство вывели университет в число передовых российских учебных заведений. По выражению Н.П. Загоскина, Лобачевский был «великим строителем» Казанского университета.

До конца 1940-х годов сведения о дате и месте рождения Н. И. Лобачевского были противоречивы. В 1948 году А.А. Андронов опубликовал статью о своих изысканиях по этому поводу, в которой указывал, что точной датой рождения математика следует считать 20 ноября 1792 года (по старому стилю), а местом — город Нижний Новгород (в 1948 году — Горький). 

Николай — средний из троих сыновей Прасковьи Александровны Лобачевской (?—1847), мужем которой был чиновник в геодезическом департаменте Иван Максимович Лобачевский (1760—1800). 

 Юность и студенческие годы.

В 1802 году Прасковья Александровна отдала всех троих сыновей в Казанскую гимназию, единственную в те годы во всей восточной части Российской империи, на «казённое разночинское содержание». Николай Лобачевский окончил гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам — латинскому, немецкому, французскому. В проявившемся уже тогда его интересе к математике — большая заслуга преподавателя гимназии Г.И. Карташевского.

Совет университета обратился к родителям воспитывающихся в Казанской гимназии детей с предложением отдать их после окончания курса гимназии для продолжения обучения в университете. П. А. Лобачевская ответила согласием. Старший брат Николая, Александр, был зачислен в университет тотчас, 18 февраля 1805 года. Николай в июле 1806 года подвергся испытанию, но неудачно, однако 22 декабря того же года прошёл повторное испытание и 14 февраля 1807 года был зачислен в университет. В том же 1807 году становится студентом Казанского университета и младший брат Николая, Алексей.

В первые годы лишь два курса года относились к физико-математическим наукам. В двух полугодиях адъюнктом И. И. Запольским читался курс физики. В первом полугодии адъюнкт Г. И. Карташевский повторил со студентами общую арифметику, прочитал курс алгебры и перешёл к изложению дифференциального исчисления. Однако 5 декабря 1806 года, из-за конфликта с директором университета И.Ф. Яковкиным, он и ряд других преподавателей были уволены. Преподавать математику было поручено студентам. Студенты вели занятия и по другим дисциплинам. В 1811 году, окончив университет, Лобачевский получил степень магистра по физике и математике с отличием и был оставлен при университете.

Геометрия Лобачевского.

Геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных состоит в том, что через точку, не лежащую на данной прямой, проходит не более чем одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её (в евклидовой геометрии такие прямые называют параллельными). В Лобачевской геометрии эта аксиома заменяется следующей: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (достаточно, чтобы это было выполнено для одной точки и одной прямой). 

В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий. Десятки работ ежегодно публикуются в этой области. Современные исследования все больше требуют делового владения геометрией Лобачевского.

Рисунок 2. Модели геометрии Лобачевского.

Другие достижения Лобачевского.

Лобачевский был не только геометром исключительной творческой силы, но и математиком с широким диапазоном научной работы. Ему принадлежит ряд фундаментальных работ в области алгебры («Алгебра или вычисление конечных», 1834, и др.) и математического анализа («Об исчезновении тригонометрических строк», 1834, «О сходимости бесконечных рядов», 1841, «О значении некоторых определённых интегралов», 1852, и др.).

В области анализа Лобачевский получил новые результаты в теории тригонометрических рядов. Им же установлен один из наиболее удобных методов приближённого решения уравнений (метод Лобачевского).

Лобачевский всю свою жизнь трудился над разработкой своей теории геометрии, но занимался и другими разделами математики.

В частности, он разработал метод приблизительного решения алгебраических уравнений и его порядка:

Лобачевского метод, метод приближённого (численного) решения алгебраических уравнений состоит в построении уравнения f1(x) = 0, корни которого являются квадратами корней исходного уравнения f(x) = 0. Затем строят уравнение f2(x) = 0, корнями которого являются квадраты корней уравнения f1(x) = 0. Повторяя этот процесс несколько раз, получают уравнение, корни которого сильно разделены.

В случае если все корни исходного уравнения действительны и различны по абсолютной величине, имеются простые вычислительные схемы для нахождения приближённых значений корней. В случае равных по абсолютной величине корней, а также комплексных корней вычислительные схемы метода Лобачевского очень сложны.

Лобачевский получил ряд ценных результатов и в других разделах математики: так, в математическом анализе получил ряд тонких теорем о тригонометрических рядах, уточнил понятие непрерывной функции:

…Общее понятие функции требует, чтобы функцией от «называть число», которое даётся для каждого и вместе с постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной…

Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе.

Метод Лобачевского — Греффе — эффективный алгоритм для нахождения корней многочлена. Иногда называется по именам первооткрывателей «Метод Лобачевского — Греффе — Данделена» или «Метод Данделена — Лобачевского — Греффе».

По сравнению с другими алгоритмами решения той же задачи (например, методом Ньютона), данный метод имеет несколько преимуществ.

Он не требует предварительной работы по выяснению, где примерно находятся корни и сколько среди них комплексных  — данный метод даёт в результате все вещественные корни, а при некоторой модификации — также и комплексные.

Недостатками метода являются отсутствие сопутствующего контроля ошибок при ручном счёте и сложность оценки точности результата.

Точность метода может оказаться невысокой из-за численной неустойчивости, то есть быстрого накопления погрешности в ходе вычислений.

Кроме того, метод медленно сходится, если у многочлена есть корни, равные или очень близкие по модулю (например, +4 и —4).

За свою жизнь Лобачевский написал большое количество трудов и научных статей. Они касались большого количества сфер: астрономии, социальной сферы, алгебры, теории вероятности, геометрии и т.д. Такие заслуги не остались незамеченными. 

Он первый доказал, что непрерывность функции и такое понятие, как дифференцированность – это не одно и то же.

Теория определителей – это также сфера математической науки, в которой Николай сделал массу исследований и открытый.

В 1892 году в России и в других странах широко отметили 100-летний юбилей Лобачевского.

Была учреждена международная премия имени Н.И. Лобачевского (1895), в Казани открыт памятник ученому. 

ГЛАВА 1. АРКИ

 1.1. Формы арочных проёмов

Основным отличительным элементом каждой арки является её свод. Именно его форма и позволяет отнести арку к той или иной разновидности. Различают следующие основные виды арок (рисунок 1):

• Классика – это наиболее распространённая разновидность, такой арочный проём гармонично впишется в любой интерьер. Свод выполняется в форме полукруга, где радиус закругления портала всегда равен половине ширины проёма.
• Романтика – такие арки имеют прямоугольные своды, углы которых скруглены. Таким образом чаще всего оформляют широкий межкомнатный проём.
• Трапеция – название говорит само за себя. Свод в трапециевидных арках выполняется в виде трапеции.
• Портал – прямоугольная арка. Наиболее проста в установке, так как не требует дополнительных трудозатрат по оформлению углов. Однако такой излишне лаконичный арочный проём будет уместен далеко не в каждом интерьере.
• Модерн – арки в таком стиле являются чем-то средним между классикой и порталом, так как округлость свода в них менее выражена, чем в классических моделях, но при этом до прямоугольной формы ещё далеко. Радиус окружности в закруглении портала может быть различным, но всегда больше половины ширины проёма. Такая разновидность арок будет гармонично выглядеть в помещениях с низкими потолками.
• Эллипс – идентична предыдущей модели, единственным отличием является больший радиус закругления на углах.

• Полуарка – является примером асимметричных арок, одна часть свода в которых повторяет арку-портал, а другая – классическую или модерн, так как радиус закругления здесь может быть абсолютно любым.

Рисунок 1. Разновидности арок по форме свода

1.2. Используемые материалы

Для изготовления арочных конструкций и оформления проемов могут использоваться различные материалы. Наиболее популярными являются:

• гипсокартон;

Гипсокартон является довольно податливым материалом, под воздействием влаги он может принимать самые различные формы, которые фиксируются после его полного высыхания. Преобразованные таким образом листы гипсокартона далее крепятся к предварительно смонтированному каркасу, изготовленному из металлических профилей с нужным радиусом закругления. Места стыка листов шпатлюются. Работать с гипсокартоном довольно просто, при наличии определённых навыков создать арочный дверной проем можно самостоятельно.

• дерево;

Деревянные арочные проёмы очень часто отличаются от обычных дверных только более широкими обналичниками. При помощи таких межкомнатных проёмов можно придать оригинальности любому интерьеру. Они отличаются высокой практичностью, так как меньше подвержены каким-либо повреждениям по сравнению со своими гипсокартонными аналогами.  Однако в результате частых перепадов влажности и температуры воздуха в помещении на них могут образовываться трещины. Но этого можно избежать, обработав древесину специальными составами

• • кирпич или камень.

Кирпичная или каменная арка является довольно интересным дизайнерским решением. Создать её можно при помощи облицовочной плитки, имитирующей кирпич или камень. Такой способ применим в тех случаях, когда необходимо декорировать уже существующий проём.

1.3 Способы декорирования

Помимо разнообразия типов конструкций и используемых материалов, арочные проемы могут дополняться различными элементами декора. Декорирование арок может выполнять несколько функций:

• Декоративную – при помощи арочного проёма усиливается эффект выбранного стилевого решения всего интерьера;
• Техническую – использование декоративных элементов позволяет несколько изменить габаритные размеры проема (высоту и ширину);
• Маскировочную – некоторые дефекты, возникшие при установке арочного проёма, можно скрыть, разместив на них элементы декора.

К декоративным элементам можно отнести:

• Карнизы — характерные элементы для арок типа классика, романтика и модерн, выполненных из дерева. Крепятся они, в основном, на стыке дугообразной и прямолинейной частей и выполняют как декоративную, так и «маскировочную» функции.
• Квадраты также характерны для деревянных арок. Они выполняют техническую функцию, так как используются в качестве элементов, позволяющих откорректировать габариты арочных конструкций. С их помощью можно увеличить ширину арок (если прикрепить их в верхней части свода) и высоту (если разместить их на стыке вертикальных составных частей). Также они являются декоративным элементом.
• Банкетки устанавливаются в основании арок и выполняют техническую и декоративную функции. Они помогают достичь нужной высоты, а также придать конструкции дополнительное изящество.
• Стыковые планки используются для маскировки стыков составных частей арок.     

1.4 Иррационально построение арок

На одном фасаде старинного здания можно увидеть следующий рисунок. В полуциркульную арку вписаны две окружности – маленькая и большая (последняя внутренним образом касается другой полуокружности, которая вместе с первой полуокружностью образует полукольцо. рис. 2,а), Измерения показали, что диаметр большей полуокружности равен 12м. Возникают вопросы: какие геометрические зависимости положены в основу этой композиции? Как, например, связаны между собой радиусы двух вписанных окружностей? Попробуем разгадать замысел средневековых архитекторов.

Из точек P и Q - концов диаметра малой полуокружности - восставим перпендикуляры до пересечения их с большей полуокружностью в точках M и N (рис. 2, б). Соединим полученные точки отрезком. Дальнейшие измерения показывают, что отношение сторон получившегося прямоугольника MNPQ равно 2:1. Тогда OP = NP. А так как радиус ON большей полуокружности равен 6, то из треугольника ONP по теореме Пифагора имеем: OP=3√2, OD= OP= 3√2.Следовательно, радиус малой окружности равен (6-3√2)/2. Отсюда отношение радиусов O₁D:O₂C окружностей равно:

 В мечети Ибн-Тулуна в Каире вместо колонн - прямоугольные столбы, соединенные стрельчатыми арками. Арки и карнизы покрывает резной растительный орнамент.

Стрельчатая арка образуется пересечением двух частей окружностей. На рис. 3 показана стрельчатая арка, в которую вписана окружность и две равные полуокружности. Измерив ширину арки, мы сможем найти не только радиус, но и длину отрезка OD, который входит в центральную часть фасада.

Обозначим радиус большой окружности через x. Тогда OO₂= x+5; DO₂=5; OB=20-x; DB=10. Дважды воспользовавшись теоремой Пифагора для треугольников ODO₂ и ODB, составим уравнение (x+5)²-5²=(20-x)²-10². Откуда x=6(м) и OO₂=6+5=11(м). А длина общего катета OD этих треугольников равна:

 ГЛАВА 1. КУПОЛА

2.1 Виды куполов

• Поясное купол

Поясное купол отличается от "настоящего купола" тем, что он состоит из отдельных горизонтальных слоев. Каждый последующий слой немного выступает над предыдущим и поддерживается консолью, в самом верху сходясь к центру.

• Купол-купол

Купол-купол имеет выпуклую форму, плавно заостряется на вершине, похожую на головку мака. Купола такой формы часто используются в строительстве храмов русской православной церкви. Такие купола имеют больший диаметр, чем основа, на котором они установлены, а их высота обычно превышает ширину.

• Овальный купол

Овальные купола является частью архитектуры барокко. Само название происходит от латинского слова ovum, что означает яйцо. Чаще овальные купола связывают с именами архитекторов Бернини и Борромини. Самый овальный купол построил в Викофорте архитектор Франческо Галло.

• Полигональный купол

Горизонтальные сечения полигональных куполов представляют собой многоугольники. Одним из известных примеров таких куполов является восьмиугольный купол собора Санта-Мария-дель-Фьоре во Флоренции, построенный Филиппо Брунеллески.

• Парусный купол

Также называемые византийскими куполами, парусные купола представляют из себя парус, основания которого не просто образуют арки для поддержки купола над ним, а сходящиеся к центру пространства, таким образом сами образуя купол. Такие купола похожи на квадратный парус, закрепленный снизу в четырех углах, и поддувает снизу.

• Купол-блюдце

Купол-блюдце представляет собой неглубокий, с малым углом между горизонталью и поверхностью у основания. Геометрически, горизонтальное сечение таких куполов есть кругом, а вертикальное - сектор круга. Купола-блюдца ниже, чем другие виды куполов.

Купола-блюдца приобрели популярность в XVIII веке, и остаются популярными по сей день. Чаще всего они используются как элемент внутреннего дизайна помещения, располагаясь в пространстве чердачных помещений

• Купол-зонтик

Купола-зонтики разделены на сегменты ребрами, расходящимися от центра к основанию купола. Материал между ребрами находится в форме арок, которые передают вертикальную нагрузку на ребра. Центральный купол Софийского собора построен по такой схеме, что позволило архитектору разместить витражи между ребрами на основании купола. Главный купол собора Святого Петра также имеет такую ​​форму.

2.2 Изготовление куполов

Изготовление металлокаркаса купола:

При изготавливаем купола, используют 2 типа материалов:

• Изготовление куполов на каркасе из конструкционной стали, прошедшей антикоррозийную обработку.
• В отдельных случаях, для изготовления купола может использоваться высококачественная нержавеющая сталь.

Облицовка купола:

Купола в соответствие с их типами и архитектурными традициями облицовываются различными способами:

• Прямая шашка
• Косая шашка
• В лемех
• В рейку
• Комбинированным способом

Для облицовки куполов мы используем следующие материалы:

• Высококачественная нержавеющая сталь декоративным покрытием:

• Золото 999 пробы, нанесённое, с помощью гальванической химии
• Нитрид титана золотистого цвета, оксидом титана под цвет свежей меди небесно-голубого или зеленых цветов и оттенков.

• Кровельная медь толщиной
• Кровельная медь с последующим покрытием сусальным золотом 980 пробы
• Оцинкованной сталью с полимерным покрытием различных цветов и оттенков.

Сборка и транспортировка:

Купола до 2,5 м в диаметре изготавливаются и облицовываются на предприятии, а затем полностью укомплектованные транспортируются на строительную площадку.

Для куполов большего диаметра используются две технологические методики изготовления и сборки, связанные, прежде всего, с возможностями транспортировки – габаритными размерами, весом каждой части и расстоянием до объекта.

В первом случае, в цеху производится изготовление и контрольная сборка металлического каркаса купола, а непосредственно сборка купола и его облицовка осуществляется уже на самом объекте, как на подготовленной площадке перед Храмом, так и непосредственно на самом Храме. Это характерно для куполов больших размеров (более 10 м в диаметре) и ограничениями по высоте и весу, связанными с возможностями подъемных механизмов.

Во втором случае, купол на производстве изготавливается сборно-разборным в виде отдельных сегментов, уже облицованных кровельными картами для удобства его перевозки, а также быстроты сборки и монтажа на строительной площадке. Кроме того, нет необходимости вести для этого бригаду кровельщиков и монтажников, а можно обойтись одним специалистом, под руководством которого, осуществляется сборка и монтаж купола с крестом на Храм.

2.3 Иррациональность построения куполов

Воплощение оригинальных архитектурных замыслов потребовало от зодчих решения целого ряда геометрических задач, приводящих к иррациональностям.

В качестве примера рассмотрим рис.5, на котором изображен вид сверху одной из среднеазиатских мечетей. Ее главная часть имеет форму прямоугольного параллелепипеда. Он перекрыт шестигранным сводом, который помещается на шести арках.

Правильное и устойчивое положение купола над вытянутым прямоугольным помещением стало возможным благодаря верно выбранному отношения сторон прямоугольника: 2:√3. Тем самым обеспечивается равенство сторон двух треугольников, пересечение которого образует шестигранную основу купола. (Сторона каждого треугольника равна √3.)

Среднеазиатские архитекторы широко использовали иррациональные числа. Приведу один пример:

Наиболее значительным зданием Средней Азии является мечеть Би-би-Ханым, которая находится в городе Самарканд. По замыслу Тимура это должно было быть самое величественное строение на земле. Вход в мечеть — через арку, между двух восьмигранных минаретов.

Свои архитекторы часто начинали с построения квадрата, стороны которого принимали за 1, а потом переходили к другим частям постройки, длины которых выражались уже иррациональными числами.

ЗАКЛЮЧЕНИЕ

Архитектура и геометрия неразделимы. Присутствие иррациональности придает любому сооружению загадочность и притягательность.  Арки всегда гармонично дополнят любое сооружение, а православные луковичные купола, благодаря своей неповторимой форме, никого не оставят равнодушным.

Порой смотришь на архитектурный шедевр и не можешь поверить, что это – творение рук человека. Каким талантом и мастерством нужно обладать, чтобы создать архитектурные памятники, совершенство которых не подвластно времени!

Рене Декарт - великий французский математик, философ, физик и механик. Он был создателем аналитической геометрии, декартовой системы координат, внес вклад в современную алгебраическую символику. Он написал такие известные философские книги: «Рассуждение о первой философии», «Рассуждение о методе» и «Первоначала философии».

После появления труда Рене Декарта «Геометрия» математика стала быстро развиваться. В нем он использовал новую математическую символику, которая позже стала общепринятой в науке. Самым главным в книге стала аналитическая геометрия, которая позволила переводить геометрические задачи на алгебраический язык с помощью системы координат.

БИОГРАФИЯ

Рене Декарт родился в городе Лаэ провинции Турень 31 марта 1596 года. Впоследствии название этого города было переименовано в «Декарт». Родители Рене были представителями старинного  дворянского рода,  обедневшего к XVI веку. В семье Рене был третьим сыном в семье. Его мать скончалась, когда ему был 1 год. Декарта воспитывала бабушка по матери, потому что отец, работающий судьей, почти все время находился в городе Ренн и очень редко навещал детей.

С самого детства Рене проявлял любознательность и стремление к знаниям. Первое образование он получил в иезуитской коллегии Ла Флеш, куда его отправили в 4 года. Эта коллегия была основана под особым покровительством Генриха IV. Его учителем был Жан Франсуа, а другом Мареном Мерсенном, ставший в будущем координатором научной жизни Франции. В этом учебном учреждении был строгий режим, но Декарту делали послабления по причине плохого здоровья.

Ла Флеш, как и большинство колледжей тогда носил религиозный характер. Такое направление системы образования зародило и укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам того времени.

После учебы в коллегии Рене получил бакалавра в области права в Пуатье и отправился в Париж, где в основном занимался математическими исследованиями. В 1617 году поступил на военную службу. Он участвовал в боях на территории Голландии во время революции и в Германии в сражении за Прагу. В Голландии Рене Декарт познакомился с физиком Исааком Бекманом, который сильно повлиял на его формирование как ученого.

Вернувшись во Францию после нескольких лет участия в войне, оказывается, что иезуиты обвинили его в ереси. Они были против его философии, угрожали ему и заставляли покинуть Францию. Декарту пришлось вернуться в Голландию в 1628 году, где он на протяжении 20 лет занимался наукой. Он изучал философию, математику, физику, астрономию и физиологию. Его прогрессивные идеи опережали уровень развития науки того времени.

За это время он написал свои знаменитые труды: «Правила по руководству ума», «Трактат о свете», «Метафизические размышления о первой философии», «Описание человечного тела» и «Начала философии». Наиболее известной стала работа «Размышление о методе». Декарт написал ее за 4 года до того, как выпустил. Он хотел отложить, а через время просмотреть и внести новые поправки. Этими поправками стало исключение того, что может вызвать недовольство церкви и смена названия на «Рассуждение о методе, чтобы хорошо направить свой разум и отыскать истину в науках. Кроме того, диоптрика, метеоры и геометрия, которые являются приложением этого метода». Чтобы с работой ознакомилось больше людей, он написал ее на французском языке, хотя очень быстро она была переведена уже и на латинский.

Современники утверждали, что в обществе Рене Декарт был высокомерным и молчаливым, предпочитал уединение компаниям, однако в кругу близких ему людей он мог проявлять активность и интерес в общении. Он всегда старался укреплять свое здоровье и даже учится владеть оружием.

К сожалению, о его личной жизни известно мало, женат он, по всей видимости, не был. Но был влюблен в служанку, от которой у него была дочь Франсина. Декарт любил дочь, и когда в пятилетнем возрасте она умерла от сильной скарлатины, он посчитал это самой большой трагедией в жизни.

За новый взгляд на науку, Рене Декарт на протяжении многих лет подвергался травле. В 1649 году он поддался уговорам шведский королевы Кристины и переехал в Стокгольм. Ей очень нравилась философия Декарта, поэтому каждое утро он лично занимался с ней философией. Сразу поле этого он простудился и умер 11 февраля 1650, предположительно от пневмонии. Но многие ученые считают, что причиной смерти стало отравление мышьяком, так как симптомы были аналогичными. Возможным поводом могло послужить вольнодумство Декарта, которое не нравилось католикам.

ВКЛАД В МАТЕМАТИКУ

Математическая символика Декарта

Декарт придумал собственную символику, с которой  было удобнее работать. Впервые она появляется в его трудах и сильно отличается от тогдашней. Многие ученые приняли и сами стали использовать эти обозначения, поэтому позже они стали общепринятыми в математике.

Именно Рене Декарт решил обозначать известные величины буквами a, b, c и т.д., а неизвестные буквами x, y, z и т.д. Все буквы в формулах Декарта считаются положительными величинами, чтобы записать отрицательную спереди ставился знак минус, а если знак был неизвестен, то спереди ставилось многоточие.

Также в трудах Декарта используется такая запись 3a, 4b, она означает, что число умножается на ту цифру, которая стоит перед переменной. Если же нужно было перемножить несколько букв, они записывались вместе.

Математик стал основателем современной записи показателя степени, именно он решил ставить его справа и чуть выше переменной: a³, b⁴. Благодаря такой записи в дальнейшем со степенями стало удобно работать. Только квадраты величин тогда обозначались так: aa, bb.

Большинство обозначений Рене Декарта были приняты, за исключением знака равенства и немного измененным знаком корня. Позже и переменные стали обозначать не только положительные, но и отрицательные величины.

Алгебраическая символика Декарта  помогла сделать вычисления более сжатыми, но при этом понятными. Именно поэтому она используется всеми уже на протяжении почти пяти столетий.

Аналитическая геометрия

В 1637 году вышла книга «Рассуждение о методе», следом за ней труд «Геометрия», в котором было дано первое изложение аналитической геометрии. Он был продолжением и состоял из 3 книг: «О задачах, которые можно построить, пользуясь только кругами, прямыми линиями», «О природе кривых линий», «О построении телесных и превосходящих телесные задач». После этих книг математики переключились с изучения числовых величин на изучение зависимостей между ними, то есть функций.

Аналитическая геометрия – раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами элементарной алгебры на основе метода координат. Это сильно укрепило связь алгебры и геометрии. Позволило решать геометрические задачи на алгебраическом языке. Основой всему этому послужила система координат.

Декартова система координат – система координат на плоскости или в пространстве, обычно взаимно перпендикулярными осями и одинаковым масштабом по осям. Она была косоугольная и координаты точек могли быть только положительными. Состояла только из осей абсцисс и ординат. Она вывела математику на новый уровень. По ней стали анализировать уравнения кривых.

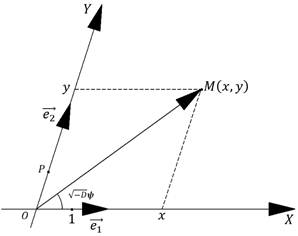
Косоугольная система координат.

Декарт впервые ввел понятие переменной величины и функции. Переменная величина – отрезок переменной длины и постоянного направления и как непрерывная числовая переменная, пробегающая совокупность чисел, составляющих координатный отрезок. Переменная величина выступала в двоякой форме, это обусловлено взаимосвязью алгебры и геометрии.

Рене Декарт изложил первую теорему в «Геометрии» в 1637 году. Эта алгебраическая теорема относится к теории расположения корней многочлена на комплексной плоскости. Теорему называют «Правило знаков Декарта». Она о том, что:

Если коэффициенты уравнения действительные и все его корни также заведомо действительные, то число его положительных корней, если учитывать их кратности, равно числу перемен знаков в ряде его коэффициентов. Если же оно именно и комплексные корни, то число это равно или на некоторое четное число меньше числа этих перемен знаков.

 ФИЛОСОФИЯ ДЕКАРТА

Философия Декарта была связана с дуализмом. Дуализм – это двойственность, душа и тело, идеальное и материальное. Сам Рене Декарт признавал в мире субстанции двух родов: протяженной и мыслящей. При этом взаимодействуют они благодаря особому источнику – Богу.

Одним из самого важного стало классическое построения философии европейского рационализма. Она стремится к абсолютно действительной и непоколебимой истине.

Использовались два противоположных подхода:

1. Эмпиризм. Опирается на чувственный опыт;
2. Мистицизм. Опирается на сверхчувственное, мистическое знание.

Философ считал, что все можно подвергнуть сомнению, чтобы отыскать настоящую истину. Один из знаменитых его афоризмов «Я мыслю, следовательно, существую».

Рене Декарт сформулировал четыре принципа в «Рассуждение о методе…», которых придерживался до конца жизни:

1. Считать истиной только то, что мыслится ясно и отчетливо;
2. Делить проблему на множество частей, чтобы полностью ее решить;
3. Исследовать более легкие предметы и постепенно восходить к познанию наиболее сложным;
4. Составлять полноценные обзоры, чтобы быть уверенным в отсутствии упущений.

Метод Декарта являлся основой его теории познания. Познание включает в себя опыт и мышление. Основополагающие врожденные истины раскрываются при помощи интеллектуальной интуиции и сомнения.

Французский математик и философ Рене Декарт сделал много открытий, проложил путь к новому, позволил наукам развиваться дальше. Он оставил необычайно большой вклад в истории. Он проложил путь следующим ученым: Паскалю, Ньютону, Арно и Николю. Четыре правила метода Декарта стали основой методов синтеза и анализа. Его влияние на развитие науки эпох нового времени огромно.

Кем же на самом деле был Леонардо да Винчи? Какое воспитание он получил, какими идеями руководствовался, каковы были его вкусы? Каким он был как художник, которого называют самым выдающимся гением за всю историю человечества? Таковы цели данной работы. Они волнуют каждого современного человека, интересующегося творчеством Леонардо да Винчи.
Внутреннюю жизнь Леонардо неизменно определяла любознательность, подобно всепожирающему огню заставляющая его захватывать с течением лет все новые и новые области знания, заниматься буквально всем, с головой погружаясь в сплошной поток штудий, исследований, экспериментов.
Живопись, получившая от Леонардо более, нежели просто ряд великолепных шедевров - от юношеского Благовещения до Дамы с горностаем и от Тайной вечери до Джоконды. Леонардо обогатил искусство живописи своей упорной проработкой, как новых методов письма, так и старинных приемов, нескончаемым совершенствованием техники рисунка и внимательным наблюдением натуры. Этот неповторимый синтез искусства, науки и технологии и является темой настоящего исследования, дающего возможность представить во всей полноте поразительную личность, символ эпохи Итальянского Возрождения.

Произведения Леонардо - это постоянная череда исследований и экспериментов. Для него живопись - это философия. Это язык, наиболее приспособленный для познания (и выражения) окружающего мира, поэтому он мог заметить: «То, что присутствует в самой сути Вселенной – настоящей или воображаемой, - художник постигает вначале сознанием, а потом исполняет с помощью рук своих, кои достойны всемирного восхищения, ибо в одно время с созданием вещей производят и согласную им гармонию». Для Леонардо искусство есть «второе» творение. С первых своих шагов студии Вероккьо художник начинает собственные творческие поиски, достигая верха совершенства в знаменитой Джоконде.

О масштабе и уникальности дарования Леонардо позволяют судить его рисунки, занимающие в истории искусства одно из почетных мест. С рисунками Леонардо да Винчи, зарисовками, набросками, схемами неразрывно связаны не только рукописи, посвященные точным наукам, но и работы по теории искусства. Много место отдано проблемам светотени, объемной моделировке, линейно и воздушной перспективе. Леонардо да Винчи принадлежат многочисленные открытия, проекты и экспериментальные исследования в математике, механике, других естественных наук.

Искусство Леонардо да Винчи, его научные и теоретические исследования, уникальность его личности прошли через всю историю мировой культуры и науки, оказали огромное влияние.
Леонардо да Винчи, из всех известных нам творцов в истории человечества, обладал наиболее всесторонней гениальностью. Он считал себя, прежде всего художником, но из его записных книжек и рисунков видно, что в свое представление об искусстве он вкладывал многое из того, что ныне мы называем естественно - научными вопросами. Он настолько был убежден в могуществе человеческого зрения как отличного инструмента для исследования природа, что видеть и знать, по его мнению, было одним и тем же.

Художники, говорил он, это лучшие из ученых; они не только наблюдают природу лучше, чем другие люди, но думают о том, что видят и затем рассказывают остальным о виденным ими в своих картинах. Нынешнее ученые предпочитают передавать свои знания в словах и для этой цели ими изобретено очень много новых слов? во времена Ренессанса считали, что "хорошая картина ценнее тысячи слов".

ИНТЕРЕСНЫЕ ФАКТЫ О ЛЕОНАРДО ДА ВИНЧИ 
Леонардо многое шифровал, чтобы его идеи раскрывались постепенно, по мере того, как человечество до них "дозреет". Изобретатель писал левой рукой и невероятно мелкими буковками, да еще и справа налево. Но и этого мало - он все буквы переворачивал в зеркальном изображении. Он говорил загадками, сыпал метафорическими пророчествами, обожал составлять ребусы. Леонардо не подписывал своих произведений, но на них есть опознавательные знаки. Например, если вглядываться в картины, можно обнаружить символическую взлетающую птицу. Таких знаков, видимо, немало, поэтому те или иные его детища вдруг обнаруживаются через века. Как было с мадонной Бенуа, которую долгое время в качестве домашней иконы возили с собой странствующие актеры.

Леонардо никогда не спешил закончить произведение, ибо неоконченность - обязательное качество жизни. Окончить - значит убить! Медлительность творца была притчей во языцех, он мог сделать два-три мазка и удалиться на много дней из города, например, благоустраивать долины Ломбардии или создавать аппарат для ходьбы по воде. Почти каждое из его значительных произведений - "незавершенка". Многие были испорчены водой, огнем, варварским обращением, но художник их не исправлял. У Мастера был особый состав, с помощью коего он на готовой картине будто специально проделывал "окна незаконченности". Видимо, так он оставлял место, куда бы сама жизнь могла вмешаться, что-то подправить.

Леонардо предпочитал метод аналогии всем другим. Приблизительность аналогии - это преимущество перед точностью силлогизма, когда из двух умозаключений неизбежно следует третье. Но одно. Зато чем причудливее аналогия, тем дальше простираются выводы из нее. Взять хоть знаменитую иллюстрацию Мастера, доказывающую пропорциональность человеческого тела. С раскинутыми руками и раздвинутыми ногами фигура человека вписывается в круг. А с сомкнутыми ногами и приподнятыми руками - в квадрат, при этом образуя крест. Такая "мельница" дала толчок ряду разнообразных мыслей. Флорентиец оказался единственным, от кого пошли проекты церквей, когда алтарь помещается посередине (пуп человека), а молящиеся - равномерно вокруг.

Рассматривая вклад Леонардо да Винчи в наследие мировой культуры и науки невозможно не отметить, насколько он опередил свое время. Остановимся на математических теориях. Изучение геометрии позволило Леонардо впервые создать научную теорию перспективы. Перспектива, - говорит да Винчи, - есть руль живописи. Она разделяется на три части:

1) укорачивание линий и углов;

2) ослабление окраски предметов находящимся между глазом зрителя и предметами слоем воздуха;

3) ослабление контуров.

Он внимательно изучил Архимеда, которого часто цитирует, и старался

пойти далее. С замечательной ясностью излагает учёный-художник в общих

чертах теорию рычага, поясняя её рисунками; не остановившись на этом, он

даёт чертежи, относящиеся к движению тел по наклонной плоскости.

Изучать творчество ученого-художника можно бесконечно. Вы сможете найти факты, которые и сегодня вызывают массу дискуссий и не трактуются однозначно.  Не имея начального образования, Леонардо да Винчи достиг высот, которые невозможно постигнуть даже в наше время.

Фрактал (от латинского «fractus» - разбитый, дробленый, сломанный) – представляет собой сложную геометрическую фигуру, которая составлена из нескольких бесконечной последовательности частей, каждая из которых подобна всей фигуре целиком, и повторяется при уменьшении масштаба.

Природа всегда поражала исследователей своей красотой и необычайностью своих изобретений. Фракталы - одно из чудес природы, о котором слышали немногие.

 В природе фрактальными свойствами обладают многие объекты: кроны деревьев, цветная капуста, облака, кровеносная и альвеолярная системы человека и животных, кристаллы, снежинки, элементы которых выстраиваются в одну сложную структуру, побережья (фрактальная концепция позволила ученым измерить береговую линию Британских островов и другие, ранее неизмеримые, объекты). Также фрактальные модели упрощают анализ движения жидкости или газа, что важно для индустриальных технологий разработки нефтегазовых месторождений.

Глава 1. Понятие «фрактал»

1. 1. История возникновения

Благодаря Мандельброту науке стало известно, как выглядит четырехмерное пространство. Оказалось, что четвертое измерение включает в себя помимо первых трех измерений, еще и интервалы между ними. В 1977 году в свет вышла книга “The Fractal Geometry of Nature”, после чего термин получил широкое распространение и заинтересовал не только специалистов, но и людей далеких от науки.

В своей книге Б.Мандельброт [3, с.15] писал: «Почему геометрию называют сухой и холодной? Одна из причин заключается в неспособности описать форму облака, горы, дерева или берега моря. Облака -это не сферы, горы-это не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой…» Бенуа Мандельброт предложил рассмотреть линию побережья с самолета, стоя на ногах и через увеличительное стекло. Во всех случаях узор будет одним и тем же, но только разного масштаба.

Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена  на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Стоит отметить, что слово «фрактал» не является математическим понятием, так же оно не имеет общепринятого строго математического определения.

Данный термин может употребляться, когда речь идет о фигуре, обладающей нижеописанными свойствами:

- фигура обладает сложной структурой при любом увеличении

- фигура является само подобной или (приближенно) само подобной

- фигура обладает дробной метрической размерностью, которая больше топологической

- фигура может быть построена рекурсивными (повторяющимися) процедурами

Фрактальная геометрия внесла неоценимый вклад в разработку новых технологий в области цифровой музыки, а также сделала возможной сжатие цифровых изображений. Фракталы широко применяются в компьютерной графике – при построении изображений деревьев, поверхности морей, горных ландшафтов, и других природных объектов. Интересно, что кроме фрактальной «живописи» существуют так же фрактальная музыка и фрактальная анимация. Фрактал, построенный по математической формуле не менее красив, чем природный.

1. 2. Классификация фракталов

Все фракталы делятся на группы. Самые крупные из них:

- алгебраические

- геометрические

- стохастические

Алгебраические. Первая группа фракталов называется алгебраической. Представители этой группы строятся на основе алгебраических формул (иногда самых простых).

Есть несколько способов получения данных фракталов:

1. фрактал Мандельброта
2. фрактал Ньютона
3. множество Жюлия

Рассмотрим, к примеру множество Мандельброта (рисунок 1).

Визуально множество Мандельброта выглядит как набор бесконечного количества различных фигур, самая крупная из них называется кардиоидой (она похожа на стилизованное изображение сердца и получила свое название от двух греческих слов — «сердце» и «вид»). Кардиоида окружена всё уменьшающимися кругами, каждый из которых окружен еще меньшими кругами, и т. д. до бесконечности. При любом увеличении данного фрактала будут выявляться всё более и более мелкие детали изображения, дополнительные ветки с более мелкими кардиоидами, кругами. И этот процесс можно продолжать бесконечно.

 Фрактал Мандельброта

Геометрические. Следующая группа носит название геометрических фракталов. По сути, именно с нее началась история фракталов. Фрактал получают с помощью какой-либо прямой, которая называется генератором. Генератор на основе правил создает нулевое поколение, после бесконечное повторение процедуры позволяет получить фрактал геометрической структуры.

Рис. 2. Кривая Коха

Последней крупной группой служат стохастические фракталы. Пожалуй, это самый привлекательный вид объектов. Такие фракталы получаются путем замены каких-либо параметров. По итогу же мы можем получить объекты, которые будут напоминать деревья, лишенные симметрии или же изрезанные береговые линии, модели рельефов местности (рисунок 3).

Стохастические фракталы

Рис.3а

Рис.3б

Рис.3в

Глава 2. ФРАКТАЛЫ ВОКРУГ НАС

2.1. Фракталы в живой природе

Все объекты, которые нас окружают, разделяются на две формы живую и не живую. Но многие не задумываются что большинство предметов, которые мы видим, само подобны. Среди растений в пример можно привести всем известное растение-папоротник или же подсолнух. А в опереньях грациозного павлина спрятаны сплошные фракталы. Так же принцип фрактальной геометрии присущ и каждому человеку. К примеру, кровь, толкаемая сердцем, движется по определённым трубочкам, которые носят название сосудов. Кровеносная система обеспечивает органы полезными веществами, необходимые для жизнеобеспечения человека, поэтому она распространяется по всему организму. Сосуды, сохраняя свое строение и структуру, становятся все более суженными и начинают разветвляться. Но это не единственная система, имеющая фрактальную структуру. Наряду с кровеносной стоят нервная и дыхательная системы, а также сетчатка глаза. Думаю, каждый человек хоть раз в жизни отправлялся в отпуск на море. Подводный мир вблизи островов очень захватывает своей красотой и уникальностью. Наряду с рыбами обитателями морей и океанов являются кораллы, морские звезды и ежи. Именно они и есть представителями фрактального подводного мира (рисунок 4).

Рис. 4.

2.2. Фракталы в неживой природе

Что касается неживой природы, так я уверена, каждый из нас в детстве, гуляя по побережью, держал в руках морскую раковину. Обычно раковины считаются сувениром, которые напоминают об отдыхе. Смотря на спиральный дом моллюсков, нет никаких сомнений в его фрактальной природе.

Приведу еще несколько примеров, которые подтверждают подлинную красоту самоподобия. В оттепель окна покрываются тонким слоем воды, которая при замерзании кристаллизуется в виде дендритов. Самые красивые -это узоры елочных веток, они представляют собой редкое красоте зрелище (рисунок 5).

Наверное, в неживой природе фрактальных изображений можно разглядеть куда больше, чем в живых формах.

Рис. 5а Ледяные узоры

Рис. 5б Раковина аммонита

Благодаря теории фракталов, иследователи стали обьяснять эволюцию галактик и развитие клеток, а создание реалистичных моделей окружающей среды позволяет рассмотреть факторы, влияющие на ее состояние. Модели, построенные на основе фрактальных изображений, позволяют с большой точностью моделировать космическое пространство и ткани внутренних органов живых организмов. Изучая данную тему и анализируя работы математических деятелей, легко обнаружить тесную взаимосвязь геометрии с красотой естественной природы. Благодаря современным возможностям интернет-ресурсов у каждого есть возможность создакть свой фрактал. Один из экспериментов по созданию фракталов на основе математической формулы представлен в презентации. Сложно поверить, что все эти прекрасные запоминающиеся фигуры скрывают за собой безликие математические формулы.

Из геометрических задач, поставленными математиками древности, выделяются три замечательные:

Удвоение куба – построить ребро куба, объем которого вдвое больше объема данного куба

Трисекция угла – разделить данный угол на три равные части

Квадратура круга – построить квадрат, площадь которого равна площади данного круга.

Автор брошюры Я И. Перельман подробно рассматривает только третью задачу-головоломку.