Последовательности. Способы задания и свойства числовых последовательностей.

Определение числовой последовательности

Числа  - элементы или члены последовательности (1)

Символ  - общий член последовательности,

А число n – его номер (1, 2, 3, 4, …, n, …)

Сокращенно последовательность (1) обозначается 

Формула, задающая  , называется формулой общего элемента (или члена)последовательности 

Например, последовательность  задана формулой = . С помощью этих формул можно вычислить любой элемент

последовательности: =1, =4, =9, …,  =100 и т.д.

Вычислите:

Можно, зная несколько первых элементов последовательности, написать формулу для общего элемента последовательности,

например: 1, , , , …, т.е. знаменатели данной последовательности образуют последовательность из квадратов нечетных

натуральных чисел, следовательно, можно выбрать формулу:

Формула, задающая  не является единственной.

Последовательность  является заданной, если указан способ получения любого ее элемента.

Часто используется рекуррентный способ задания последовательности :

1. дается первый элемент последовательности или несколько первых элементов;

2. формула (или рекуррентное соотношение), указывающая, какие действия нужно выполнить, чтобы вычислить следующий элемент,

или несколько следующих элементов.

Таким образом, чтобы задать последовательность, недостаточно написать только рекуррентное соотношение, необходимо указать

также начальные члены последовательности.

Действия над последовательностями:

учебник Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учеб. для студ.

учреждений сред.проф. образования/ М.И. Башмаков. – 4-е изд.,стер. – М. : ИЦ «Академия», 2017, - 256 с.

Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности.

Числовую последовательность, иногда, рассматривают как функцию числового аргумента. Иначе говоря, каждому натуральному

числу n поставлено в соответствие действительное число  .

Числовые последовательности могут обладать свойствами обычных функций.

Возрастающие и убывающие последовательности

•  Числовую последовательность  x₁ ,  x₂ , … x_n , …

называют возрастающей последовательностью, если каждый член этой последовательности больше предшествующего члена

т.е.  для всех   n = 1, 2, 3, …   выполнено неравенство

x_{n + 1} > x_{n  ,}  например, последовательность натуральных чисел

1, 2, 3, … n, … является возрастающей последовательностью.

•  Числовую последовательность  x₁ ,  x₂ , … x_n , …, называют убывающей последовательностью, 

если каждый член этой последовательности меньше предшествующего члена

т.е. для всех   n = 1, 2, 3, …   выполнено неравенство

x_n +1 < x_n , например, последовательность   заданная формулой   

 является убывающей последовательностью.

Числовая последовательность 1, – 1, 1, – 1, … заданная формулой

x_n = (– 1)ⁿ,       n = 1, 2, 3, … не является ни возрастающей, ни убывающей последовательностью.

• Возрастающие и убывающие числовые последовательности  называют монотонными  последовательностями.

• Числовую последовательность x₁ ,  x₂ , … x_n , … ,

называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M.

Другими словами, для всех   n = 1, 2, 3, …   выполнено неравенство x_n < M

• Числовую последовательность   x₁ ,  x₂ , … x_n , … называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m: для всех   n = 1, 2, 3, …   выполнено неравенство x_n > m,

Например, числовая последовательность 1, 4, 9, … n² , … заданная формулой x_n = n²,       n = 1, 2, 3, … , ограничена снизу, например, числом 0.  Однако эта последовательность неограничена сверху.

• Числовую последовательность x₁ ,  x₂ , … x_n , …, называют ограниченной, если она ограничена и сверху, и снизу.

Другими словами, существуют такие числа M и m, что для всех   n = 1, 2, 3, …   выполнено неравенство m < x_n < M

Например, последовательность    заданная формулой   является ограниченной последовательностью,

поскольку для всех   n = 1, 2, 3, …   выполнено неравенство   

•  Числовые последовательности, которые не являются ограниченными, называют неограниченными последовательностями.      

• Число   a   называют пределом числовой последовательности a₁ ,  a₂ , … a_n , …  если для любого

положительного числа   ε>0   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство | a_n – a | < ε .

Условие того, что число   a   является пределом числовлй последовательности    a₁ ,  a₂ , … a_n , … , записывают с помощью обозначения

(читается как: «Предел   a_n   при   n,   стремящемся к бесконечности, равен   a ».) То же самое соотношение можно записать

следующим образом: a_n → a   при  (читается как: «a_n   стремится к   a   при   n,   стремящемся к бесконечности»).

Замечание. Если для последовательности a₁ ,  a₂ , … a_n , … найдется такое число   a ,   что   a_n → a   при ,

то эта последовательность ограничена

Свойства пределов различных последовательностей

Последовательность  a₁ ,  a₂ , … a_n , … стремится к бесконечности, если для любого положительного числа   C  

найдется такое натуральное число   N,   что при всех   n > N   выполняется неравенство | a_n| > C .

Условие того, что числовая последовательность

a₁ ,  a₂ , … a_n , … , стремится к бесконечности, записывают с помощью обозначения         или с помощью

обозначения  при 

1.  Для любого числа   k > 0   справедливо равенство  

2 . Для любого числа   k > 0   справедливо равенство   

3. Для любого числа   a   такого, что   | a | < 1,   справедливо равенство         

4. Для любого числа   a   такого, что   | a | > 1,   справедливо равенство             

5 . Последовательность – 1 , 1 , – 1 , 1 , … , заданная с помощью формулы общего члена  a_n = (– 1)ⁿ , предела не имеет.

      Рассмотрим две последовательности

a₁ ,  a₂ , … a_n , … ,   и   b₁ ,  b₂ , … b_n , … .

Если при    существуют такие числа   a   и   b ,  что

   и   

 существуют также и пределы суммы, разности и произведения этих последовательностей, причем

 Если, кроме того, выполнено условие      то при  существует предел дроби     причем

Нахождение пределов числовых последовательностей

Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремится к 

то вычисление такого предела называют раскрытием неопределенности типа 

Часто неопределенность типа  удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки

«самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены,

«самым большим» слагаемым будет член с наивысшей степенью.

      Пример. Найти предел последовательности

      Решение. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней

      Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби,

а также, используя свойства пределов последовательностей    при |а|<1,  получаем

      Ответ. 

Комплексные числа

Числа вида z=a+bi, где  a и b – действительные числа, а  i – мнимая единица называются комплексными

i – мнимая единица

i² = -1,

i

Рассмотрим степени числа i

i¹ = i

i² = -1

i³ = i² * i = -1 * i = - i

i⁴ = i² * i² = -1 * (-1) = 1

Данная последовательность степеней числа i повторяется

Используя закономерность, легко найти значение степени числа i

Задачи на нахождение значения степени i

Найти i²⁸

Найти i³³

Найти i¹³⁵

Найти i⁶⁶

Число а – действительная часть комплексного числа (Re z)

bi – мнимая часть комплексного числа (Im z)

b – коэффициент при мнимой части

Запись комплексного числа в виде z=a+bi называется алгебраической формой комплексного числа

Противоположные комплексные числа: z=a + bi     и    –z= – a – bi

Действия над комплексными числами в алгебраической форме

z₁=2 + 3i

z₂=5 – 7i

1. Сложение

сложить действительные и мнимые части чисел

z₁ + z₂ = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i = (2 + 5) + (3i + (-7i))= 7 – 4i

2. Вычитание

вычесть действительные и мнимые части

z₁ –  z₂ = (2 + 3i) – (5 – 7i) = (2 – 5) + (3i – (-7i)) = - 3 + 10i

3. Умножение

по правилу умножение многочленов («фонтанчиком»)

z₁ * z₂ = (2 + 3i) * (5 – 7i) = 10 – 14i + 15i – 21i² = (10 + 21) + (– 14i + 15i) = 31+ i

 (– 21i²) = - 21 *(-1) т.к. i² = -1

При выполнении умножения можно использовать формулы сокращенного умножения

Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью

4. Деление

Чтобы выполнить деление двух комплексных чисел, нужно и делимое и делитель умножить на комплексное число,

сопряженное делителю, например:

При решении учитываем i² = -1

Следующий пример:

Решение квадратных уравнений, дискриминант которых отрицательный

На множестве С любое квадратное уравнение имеет корни

Пример:

Решить уравнение на множестве комплексных чисел

Таким образом, уравнение        на множестве C имеет ровно два различных комплексных корня:  

Решить уравнение:

i – начальная буква французского слова «imaginaire» - мнимый

(Математика: Учебное пособие / Под  ред. М.М.  Чернецова.  — М.: РГУП, 2015.)

Контрольные вопросы «Абсолютная погрешность и ее граница. Верные цифры числа.

Относительная погрешность и ее граница. Приближенные вычисления; действия

с приближенными значениями вычислений. Вычисления с наперед заданной точностью»

Ответы: I вариант

Решение I вариант

При извлечении корня сохраняют столько значащих цифр, сколько их в подкоренном выражении, однако,

по условию задачи необходимо взять приближенные значения корней с точностью до 0,001, тогда

 – учитываем точность

   (∆а = 0,001)

2. Площадь параллелограмма вычисляется по формуле

S=a*h, в условии даны измерения со всеми значащими цифрами

a = 68,7 (значит ∆а = 0,5)

h = 52,6 (значит ∆h = 0,5)

S=a*h = 68,7 * 52,6 = 3613,62 используем правило округления до значащих цифр

S = 3610

Чтобы указать значащие цифры, необходимо знать границу абсолютной погрешности площади ∆S

 - граница абсолютной погрешности произведения        

Это значит, что S = 3600 (3600±72) и верные цифры 3 и 6

3. а = 7,36 ± 0,004, здесь ∆а = 0,004

b = 8,61 ± 0,005, здесь ∆b = 0,005

a*b= 7,36 * 8,61 = 63,3696   

Окончательно:  a*b = 63,4 ± 0,1

4.    испоользуем формулу относительной погрешности для квадратного корня

5. R = 8,  

S=π*R² – площадь круга, если учитывать приближенное значение числа π как константу, то используем формулу

границы относительной погрешности квадрата, тогда

 , запишем границу относительной погрешности, равную 0,5%, как 0,005 и решим неравенство

  ,значит точность измерения радиуса круга 0,02 м

Примеры решения задач

В а р и а н т    2.     1.       2. 0,750     3. 9,1 ± 0,35

Краткий конспект для подготовки к зачету

или здесь

https://math4everyone.info/media/metod/%D0%9B%D0%B8%D1%81%D0%B8%D1%87%D0%BA%D0%B8%D0%BD_%D0%A1%D0%BE%D0%BB%D0%BE%D0%B2%D0%B5%D0%B9%D1%87%D0%B8%D0%BA-84-112.pdf

Геометрическая интерпретация производной, впервые данная в конце XVII века Лейбницем, состоит в следующем:

Значение производной функции y=f(x) в точке x равно угловому коэффициенту касательной, проведенной к графику

функции в той же точке x, т.е.                k = f ’(x) = tg φ

Рассмотрим задачу.

Определение: прямая, проходящая через точку касания, перпендикулярно касательной,

называется нормалью к кривой в этой точке.

Если кривая определена уравнением  , то уравнение касательной к ней в точке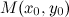   

имеет вид:

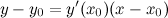
а уравнение нормали:

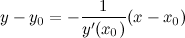
Как Вы заметили нам нужно найти производную, чтобы написать уравнение касательной или нормали. 

Операцию отыскания производной некоторой функции называется дифференцированием функции, а раздел математики, изучающий свойства этой операции, - дифференциальным исчислением. Если функция имеет производную в точке х=а, то говорят, что она дифференцируема в этой точке. Если функция имеет производную в каждой точке данного промежутка, то говорят, что она дифференцируема на этом промежутке.

Существуют общие правила нахождения производной:

(в пояснении   – это у(x +∆x)  )

Применим эти правила и найдем производную функции y=5x

1. y(x +∆x)  = 5(x +∆x) = 5x + 5∆x
2. ∆y = y(x +∆x) –  y(x) = (5x + 5∆x) – 5x = 5∆x
3.    =   = 5
4. 

Таким образом, мы нашли производную функции, пользуясь непосредственным определением производной.

Но это не очень удобно, хотя и позволяет вычислить производную любой элементарной функции.

Вспомним, элементарные функции — функции, которые можно получить с помощью конечного числа

арифметических действий и композиций из следующих основных элементарных функций: степенная функция 

с любым действительным показателем; показательная и логарифмическая функции; тригонометрические и обратные

тригонометрические функции.

Формулы производных основных элементарных функций

Правила вычисления производных

Вычисление производных основано на применении следующих правил, которые мы будем использовать

Правило 1 (производная от произведения числа на функцию).

Справедливо равенство            (c f (x))' = c f ' (x) , где  c – любое число.

Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.

Правило 2 (производная суммы функций).

Производная суммы функций вычисляется по формуле

(f (x) + g (x))' = f ' (x) + g' (x),

то есть производная от суммы функций равна сумме производных этих функций.

Правило 3 (производная разности функций).

Производная разности функций вычисляется по формуле 

(f (x) – g (x))' = f ' (x) – g' (x),

то есть производная от разности функций равна разности производных этих функций.

Правило 4 (производная произведения двух функций).

Производная произведения двух функций вычисляется по формуле

(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x),

Другими словами, производная от произведения двух функций равна производной от первой функции,

умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.

Правило 5 (производная частного двух функций).

Производная от дроби (частного двух функций) вычисляется по формуле

Рациональные неравенства.

1. Дробно-рациональные неравенства

Список использованных интернет-ресурсов:

1. https://urait.ru/

Действия над комплексными числами (в тригонометрической и показательной форме)

  – тригонометрическая форма записи комплексного числа

  – показательная форма записи комплексного числа

(Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие))

При решении примеров надо знать значения тригонометрических функций. Как найти значения тригонометрических функций► пройди по ссылке⇒

https://math4everyone.info/math/kak-najti-znacheniya-sinusa-kosinusa-tangensa-i-kotangensa-s-pomoshyu-edinichnoj-okruzhnosti/

Примеры

Даны комплексные числа

Найти:

Решение:

Даны комплексные числа

Найти:

Решение:

Показательная форма комплексного числа

Если комплексному числу

 , где r = 1 поставить в соответствие показательное выражение      ,

то получим соотношение

  – которое называется формулой Эйлера.

Любое комплексное число z можно записать в виде

Это - показательная форма записи комплексного числа 

Существует три формы записи комплексного числа:

  - алгебраическая форма

  - тригонометрическая форма

  - показательная форма

Как записать комплексное число в показательной форме?

Если комплексное число записано в тригонометрической форме, то поступим следующим образом:

Записать комплексное число z=-5i  в тригонометрической и показательной формах

Записать комплексное число в тригонометрической и показательной формах

Записать комплексное число в алгебраической и показательной формах

Записать комплексное число в алгебраической и тригонометрической формах

Как изобразить комплексное число на координатной плоскости

Комплексное число z = a + bi можно изобразить на координатной плоскости точкой Z с координатами (a;b)

Действительные часть числа координата Х=а откладывается по оси абсцисс – ОХ (действительная ось),

мнимая часть числа координата У=b по оси ОУ (мнимая ось)

Комплексное число также можно изобразить в виде вектора        с началом в точке О(0;0) и концом в точке Z(a;b)

Тригонометрическая форма комплексного числа

Комплексное число z = a + bi изображено в виде вектора   с началом в точке О(0;0) и концом в точке Z(a;b)

Модуль комплексного числа – это длина вектора  , которую можно найти по формуле

Аргумент комплексного числа – это угол ᵠ , который образует вектор  с положительным направлением оси абсцисс (ОХ)

Величину этого угла можно найти из соотношений в прямоугольном треугольнике

Из соотношений следует    

Тогда мы получим тригонометрическую форму записи комплексного числа

Окончательно

Как перейти от алгебраической формы записи комплексного числа к тригонометрической:

1. Найти модуль комплексного числа r

2. Определить в какой четверти координатной плоскости находится точка Z, чтобы найти ᵠ

3. Составить уравнение                 и найти угол ᵠ
4. Записать комплексное число z в тригонометрической форме

Например:

Записать в тригонометрической форме комплексное число

Решение:

1. a=1, b= - 1

Точка Z находится в IV четверти

Этим соотношениям соответствует в IV четверти угол     

4. Запишем тригонометрическую форму комплексного числа:

Записать в тригонометрической форме комплексное число

Решение:

1. a= -1, b=   

Точка Z находится во II четверти

Этим соотношениям соответствует во II четверти угол      или 120^о

4. Запишем тригонометрическую форму комплексного числа:

   или   

Для самоподготовки

Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)