Математический анализ
Геометрическая интерпретация производной, впервые данная в конце XVII века Лейбницем, состоит в следующем:
Значение производной функции y=f(x) в точке x равно угловому коэффициенту касательной, проведенной к графику
функции в той же точке x, т.е. k = f ’(x) = tg φ
Рассмотрим задачу.
Определение: прямая, проходящая через точку касания, перпендикулярно касательной,
называется нормалью к кривой в этой точке.
Если кривая определена уравнением  , то уравнение касательной к ней в точке
, то уравнение касательной к ней в точке 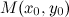
имеет вид:
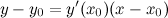
а уравнение нормали:
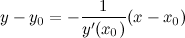
Как Вы заметили нам нужно найти производную, чтобы написать уравнение касательной или нормали.
Операцию отыскания производной некоторой функции называется дифференцированием функции, а раздел математики, изучающий свойства этой операции, - дифференциальным исчислением. Если функция имеет производную в точке х=а, то говорят, что она дифференцируема в этой точке. Если функция имеет производную в каждой точке данного промежутка, то говорят, что она дифференцируема на этом промежутке.
Существуют общие правила нахождения производной:
(в пояснении – это у(x +∆x) )
Применим эти правила и найдем производную функции y=5x
- y(x +∆x) = 5(x +∆x) = 5x + 5∆x
- ∆y = y(x +∆x) – y(x) = (5x + 5∆x) – 5x = 5∆x
-
=
= 5
Таким образом, мы нашли производную функции, пользуясь непосредственным определением производной.
Но это не очень удобно, хотя и позволяет вычислить производную любой элементарной функции.
Вспомним, элементарные функции — функции, которые можно получить с помощью конечного числа
арифметических действий и композиций из следующих основных элементарных функций: степенная функция
с любым действительным показателем; показательная и логарифмическая функции; тригонометрические и обратные
тригонометрические функции.
Формулы производных основных элементарных функций
Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать
Правило 1 (производная от произведения числа на функцию).
Справедливо равенство (c f (x))' = c f ' (x) , где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций).
Производная суммы функций вычисляется по формуле
(f (x) + g (x))' = f ' (x) + g' (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций).
Производная разности функций вычисляется по формуле
(f (x) – g (x))' = f ' (x) – g' (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций).
Производная произведения двух функций вычисляется по формуле
(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x),
Другими словами, производная от произведения двух функций равна производной от первой функции,
умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций).
Производная от дроби (частного двух функций) вычисляется по формуле