Глава 1. ЖИЗНЬ БЛЕЗА ПАСКАЛЯ.

1.1. Детство.

Паскаль родился в городе Клермон-Ферран (французская провинция Овернь) в семье председателя налогового управления Этьена Паскаля и Антуанетты Бегон, дочери сенешаля Оверни. У Паскалей было трое детей — Блез и две его сестры: младшая — Жаклин и старшая — Жильберта. Мать умерла, когда Блезу было 3 года. В 1631 году семья переехала в Париж.

Блез рос одарённым ребёнком. Его отец Этьен самостоятельно занимался образованием мальчика; Этьен и сам неплохо разбирался в математике — дружил с Мерсенном и Дезаргом, открыл и исследовал неизвестную ранее алгебраическую кривую, с тех пор получившую название «улитка Паскаля», входил в комиссию по определению долготы, созданную Ришельё.

Паскаль-отец придерживался принципа соответствия сложности предмета умственным способностям ребёнка. По его плану древние языки Блез должен был изучать с 12 лет, а математику с 15-16-летнего возраста. Метод обучения состоял в объяснении общих понятий и правил и последующем переходе к изучению отдельных вопросов. Так, знакомя восьмилетнего мальчика с законами грамматики, общими для всех языков, отец преследовал цель научить его мыслить рационально. В доме постоянно велись беседы по вопросам математики и Блез просил познакомить его с этим предметом. Отец, опасавшийся, что математика помешает сыну изучать латинский и греческий языки, обещал в будущем познакомить его с этим предметом. Как-то раз, на очередной вопрос сына о том, что такое геометрия, Этьен кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции, однако запретил ему всякие исследования в этой области. Однако Блез, оставаясь один, принялся углём чертить на полу различные фигуры и изучать их. Не зная геометрических терминов, он называл линию «палочкой», а окружность «колечком». Когда отец случайно застал Блеза за одним из таких самостоятельных уроков, он был потрясён: мальчик, не знавший даже названий фигур, самостоятельно доказал 32-ю теорему Евклида о сумме углов треугольника. По совету своего друга Ле Пайера Этьен Паскаль отказался от своего первоначального плана обучения и разрешил читать сыну математические книги. В часы отдыха Блез изучал Евклидову геометрию, позднее, с помощью отца, перешёл к работам Архимеда, Аполлония и Паппа, потом — Дезарга.

В 1634 году (Блезу было 11 лет), кто-то за обеденным столом зацепил ножом фаянсовое блюдо. Оно зазвучало. Мальчик обратил внимание, что стоило прикоснуться к блюду пальцем, как звук исчез. Чтобы найти этому объяснение, Паскаль провёл серию опытов, результаты которых позднее изложил в «Трактате о звуках».

С 14 лет Паскаль участвовал в еженедельных семинарах Мерсенна, проводимых по четвергам. Здесь он познакомился с Дезаргом. Юный Паскаль был одним из немногих, кто изучал его труды, написанные сложным языком и насыщенные новоизобретёнными терминами. Он совершенствовал идеи, высказанные Дезаргом, обобщая и упрощая обоснования.

В 1640 году выходит первое печатное произведение Паскаля — «Опыт о конических сечениях», результат исследования работ Дезарга. В это сочинение автор включил теоремы (доказательства не приводятся), три определения, три леммы и указал главы планируемого труда, посвящённого коническим сечениям. Третья лемма из «Опыта…» является теоремой Паскаля: если вершины шестиугольника лежат на некотором коническом сечении, то три точки пересечения прямых, содержащих противоположные стороны, лежат на одной прямой. Этот результат и 400 следствий из него Паскаль изложил в «Полном труде о конических сечениях», о завершении которого Паскаль сообщил пятнадцать лет спустя и который сейчас отнесли бы к проективной геометрии. «Полный труд…» так и не был опубликован: в 1675 году его прочёл в рукописи Лейбниц, рекомендовавший племяннику Паскаля Этьену Перье срочно напечатать его. Однако Перье не прислушался к мнению Лейбница, впоследствии рукопись была утеряна.

1.2. Личность. 

Блез Паскаль был чрезвычайно скромным и необыкновенно добрым человеком, а его биография полна примерами удивительной жертвенности.

Он бесконечно любил бедных и всегда старался им помочь даже (и чаще всего) в ущерб себе. Его друзья вспоминают: «Он никогда никому не отказывал в милостыне, хотя сам был небогат и расходы, которых требовали его частые недуги, превышали его доходы. Он всегда давал милостыню, отказывая себе в необходимом. Но когда ему на это указывали, в особенности, когда его траты на милостыню бывали очень велики, он огорчался и говорил нам: «Я заметил, что как бы ни был человек беден, после его смерти всегда что-то остается». Порой он заходил так далеко, что ему приходилось занимать на жизнь и брать в долг с процентами, чтобы иметь возможность раздавать бедным все, что у него было; после этого он ни за что не хотел прибегать к помощи друзей, потому что он взял себе за правило никогда не считать чужие нужды обременительными для себя, но всегда остерегаться обременять своими нуждами других».

Осенью 1661 года Паскаль поделился с герцогом де Роанне идеей создания дешёвого и доступного для бедных людей способа передвижения в многоместных каретах. Герцог оценил проект Паскаля, и через год в Париже открылся первый маршрут общественного транспорта, названного впоследствии омнибусом.

Незадолго до смерти, Блез Паскаль принял в свой дом семью бедняка, который не мог платить за жилье. Когда один из сыновей этого бедняка заболел ветрянкой, Паскалю посоветовали на время удалить из дома больного мальчика.

Но Блез, будучи уже сам тяжело больным, сказал, что для него переезд менее опасен, чем для ребенка, и попросил, чтобы лучше его перевезли к сестре, хотя это стоило для него больших трудностей. Таков был Паскаль. 

1.3. Поздние годы.

С 1658 года здоровье Паскаля быстро ухудшается. Его одолевает физическая слабость, появляются ужасные головные боли. Гюйгенс, посетивший Паскаля в 1660 году, нашёл его глубоким стариком, несмотря на то, что в тот момент Паскалю было всего 37 лет. Паскаль понимает, что скоро умрёт, но не испытывает страха перед смертью, говоря сестре Жильберте, что смерть отнимает у человека «несчастную способность грешить». Не имея возможности ни читать, ни писать, ни размышлять, он занимается благотворительностью и изредка посещает старых друзей.

В октябре 1661 года умирает сестра Жаклин. Это был тяжёлый удар для Паскаля. 19 августа 1662 года после мучительной продолжительной болезни Блез Паскаль скончался. Похоронен в приходской церкви Парижа Сен-Этьен-дю-Мон.

Глава 2. ДОСТИЖЕНИЯ ПАСКАЛЯ В МАТЕМАТИКЕ.

2.1. «Паскалина». Суммирующая машина Паскаля, «Паскалина» — арифметическая машина, изобретённая французским учёным Блезом Паскалем (1623—1662) в 1642 году.

 "Паскалина"

Француз Блез Паскаль начал создавать суммирующую машину «Паскалину» в 1642 году в возрасте 19 лет, наблюдая за работой своего отца, который был сборщиком налогов и часто выполнял долгие и утомительные расчёты.

Машина Паскаля представляла собой механическое устройство в виде ящичка с многочисленными связанными одна с другой шестерёнками. Складываемые числа вводились в машину при помощи соответствующего поворота наборных колёсиков. На каждое из этих колёсиков, соответствовавших одному десятичному разряду числа, были нанесены деления от 0 до 9. При вводе числа колесики прокручивались до соответствующей цифры. Совершив полный оборот, избыток над цифрой 9 колёсико переносило на соседний разряд, сдвигая соседнее колесо на 1 позицию. Первые варианты «Паскалины» имели пять зубчатых колёс, позднее их число увеличилось до шести или даже восьми, что позволяло работать с большими числами, вплоть до 9 999 999. Ответ появлялся в верхней части металлического корпуса. Вращение колёс было возможно лишь в одном направлении, исключая возможность непосредственного оперирования отрицательными числами. Тем не менее машина Паскаля позволяла выполнять не только сложение, но и другие операции, но требовала при этом применения довольно неудобной процедуры повторных сложений. Вычитание выполнялось при помощи дополнений до девятки, которые для помощи считавшему появлялись в окошке, размещённом над выставленным оригинальным значением.

Несмотря на преимущества автоматических вычислений, использование десятичной машины для финансовых расчётов в рамках действовавшей в то время во Франции денежной системы было затруднительным. Расчёты велись в ливрах, су и денье. В ливре насчитывалось 20 су, в су — 12 денье. Использование десятичной системы в недесятичных финансовых расчётах усложняло и без того нелёгкий процесс вычислений.

Тем не менее примерно за 10 лет Паскаль построил около 50, и даже сумел продать около дюжины вариантов своей машины. Несмотря на вызываемый ею всеобщий восторг, машина не принесла богатства своему создателю. Сложность и высокая стоимость машины в сочетании с небольшими вычислительными способностями служили препятствием её широкому распространению. Тем не менее, заложенный в основу «Паскалины» принцип связанных колёс почти на три столетия стал основой для большинства создаваемых вычислительных устройств.

Машина Паскаля стала вторым реально работающим вычислительным устройством после считающих часов  Вильгельма Шикарда, созданных в 1623 году.

Переход Франции в 1799 году на метрическую систему коснулся также её денежной системы, которая стала, наконец, десятичной. Однако практически до начала XIX века создание и использование считающих машин оставалось невыгодным. Лишь в 1820 году Шарль Ксавье Тома де Кольмар запатентовал первый механический калькулятор, ставший коммерчески успешным.

2.2. Треугольник Паскаля

Треугольник Паскаля  — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.

Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика  X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольштадтского университета, также изображён треугольник Паскаля. А в 1653 году (в других источниках в 1655 году или в 1665 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике».

Основные свойства Треугольник Паскаля поражает своим совершенством. Для любой строки под номером n (n = 0, 1, 2…) верно: первое и последнее числа — 1; второе и предпоследнее — n; третье число равно треугольному числу (количеству кружков, которые можно расставить в виде равностороннего треугольника, четвертое число является тетраэдрическим, т. е. представляет собой пирамиду с треугольником в основании. Кроме того, сравнительно недавно, в 1972 году, было установлено еще одно свойство треугольника Паскаля. Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом. ₽ Ткань лён от 1м по оптовым ценам Быстрая олимпиада для аттестации! Тот же трюк можно осуществить и по-другому. Для этого в треугольнике Паскаля заменяют числа на остатки от их деления на номер строки в таблице. Затем располагают строки в полученном треугольнике так, чтобы следующая из них начиналась правее на 2 колонки от первого элемента предыдущей. Тогда столбцы, имеющие номера, являющиеся простыми числами, будут состоять только из нулей, а в тех, у которых они составные, будет присутствовать хотя бы один ноль.

2.3. Опыт о конических сечениях.

Опыт о конических сечениях (Essai pour les coniques, 1639) — теорема Паскаля о том, что во всяком шестиугольнике, вписанном в эллипс, гиперболу или параболу, точки пересечения трёх пар противоположных сторон лежат на одной прямой.

Трактат включает в себя три определения, три леммы, несколько теорем (без доказательств) и наименования глав предполагаемого обширного труда по коническим сечениям. Паскаль здесь отдает дань признательности своему учителю, называя Дезарга одним из великих умов своего времени, одним из лучших математиков и знатоков теории конических сечений. «Я хочу заявить, — пишет Паскаль, — что немногим мной найденным в этих вопросах я обязан его сочинениям и что я старался, насколько это было возможно, подражать его методу». Тем не менее небольшой трактат Паскаля вполне самостоятелен и оригинален. Паскаль в своем «Опыте...» дает формулировку одной из основных теорем проективной геометрии, которую восхищенный Дезарг назвал «великой Паскалевой теоремой»:

три точки пересечения противоположных сторон шестиугольника, вписанного в коническое сечение, лежат на одной прямой.

Согласно третьей лемме, во всяком шестиугольнике (его автор трактата называет «мистическим шестивершинником»), вписанном в эллипс, гиперболу или параболу, точки пересечения трех пар противоположных сторон лежат на одной прямой, называемой теперь прямой Паскаля.

Если шесть произвольных точек конического сечения принять за вершины шестиугольника и занумеровать их, то противоположные стороны данного шестиугольника (1, 2) и (4, 5); (2, 3) и (5, 6); (3, 4) и (6, 1) пересекутся соответственно в точках Р, Q, R, которые лежат на одной прямой — прямой Паскаля .

По словам Мерсенна, Блез вывел из своей фундаментальной теоремы около четырехсот различных следствий. Вот одно из самых простых, но и самых важных следствий:

«Коническое сечение однозначно определяется любыми своими пятью точками. Действительно, пусть 1, 2, 3, 4, 5 — точки конического сечения и m — произвольная прямая, проходящая через (5). Тогда на m существует единственная точка (6) конического сечения, отличная от (5). В обозначениях теоремы Паскаля точка Р является точкой пересечения (1, 2) и (4, 5), Q — точка пересечения (2, 3) и m, R — точка пересечения (3, 4) и (Р, Q), a тогда (6) определится как точка пересечения (I, R) и m».

Глава 3. ПАРИ  ПАСКАЛЯ.

В произведении Паскаля «Мысли» есть текст, известный как «Пари Паскаля». Уже почти 400 лет философы и ученые дискутируют по поводу этого «спора», в котором ученый утверждает, что от ответа на вопрос «есть Бог или нет?» зависит вечная участь человека. Поскольку нет никаких рациональных доводов, окончательно утверждающих Его бытие или небытие, то выбор исключительно за нами. Чтобы ничего не проиграть и выиграть пари, по мысли Паскаля, «выгоднее» верить в Него и жить по заповедям.

Приведем текст «Пари» полностью.

«Да, но если это извиняет тех, кто говорит, что религия не доказываема, и снимает с них упрек в непредставлении доказательств, то это самое не оправдывает принимающих ее». Исследуем этот пункт и скажем: Бог есть или Бога нет. Но на которую сторону мы склонимся? Разум тут ничего решить не может. Нас разделяет бесконечный хаос. На краю этого бесконечного расстояния разыгрывается игра, исход которой не известен. На что вы будете ставить? Разум здесь ни при чем, он не может указать вам выбора. Поэтому не говорите, что сделавшие выбор заблуждаются, так как ничего об этом не знаете. «Нет; но я порицал бы их не за то, что они сделали тот или другой выбор, а за то, что они вообще решились на выбор; так как одинаково заблуждаются и выбравшие чет, как и выбравшие нечет. Самое верное — совсем не играть». Да, но делать ставку необходимо: не в вашей воле играть или не играть. На чем же вы остановитесь? Так как выбор сделать необходимо, то посмотрим, что представляет для вас меньше интереса: вы можете проиграть две вещи, истину и благо, и две вещи вам приходится ставить на карту, ваши разум и волю, ваше познание и ваше блаженство; природа же ваша должна избегать двух вещей: ошибки и бедствия. Раз выбирать необходимо, то ваш разум не потерпит ущерба ни при том, ни при другом выборе. Это бесспорно; ну, а ваше блаженство? Взвесим выигрыш и проигрыш, ставя на то, что Бог есть. Возьмем два случая: если выиграете, вы выиграете все; если проиграете, то не потеряете ничего. Поэтому, не колеблясь, ставьте на то, что Он есть (В. Паскаль. «Мысли» (М., 1902), Перевод с французского О. Долгова. Подбор произведен В. И. Кузнецовым, С. 64—65).

         В этом виден великий философ Блез Паскаль. Наряду с научными познаниями, ученые того времени искали первопричины мироздания. Так как наука не может строится отдельно от бытия. И нельзя только научными методами объяснить все происходящее в окружающем нас мире.

ЗАКЛЮЧЕНИЕ.

На основе всего вышесказанного, можно сделать вывод, что великий математик, физик, философ и литератор Блез Паскаль действительно внес большой вклад в человеческие жизни.

История жизни Паскаля не только раскрывает судьбу одного из гениальнейших людей, но и учит настоящим ценностям — любви к ближнему, поиске духовного и самоотверженной работе над собой. Именно Паскалю пришла идея оценить вероятность различных исходов при игре в кости. Если ученые древности считали подобный исход только удачей, то Паскаль использовал числовой треугольник, который был назван в его честь.

[Читал] чудного Паскаля… человека великого ума и великого сердца… не мог не умилиться до слез, читая его и сознавая своё полное единение с этим умершим сотни лет тому назад человеком.  (Лев Толстой)

Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения.

Пирамида как геометрическая форма — пожалуй, одно из самых совершенных в природе. Интерес к пирамидам все больше и больше возрастает. Изучением пирамид занимались многие археологи, ученые, математики и каждый из них открывал новые свойства этих сооружений. По сей день существует еще много загадок, связанных с пирамидами. Разгадать их еще предстоит будущим поколениям ученых и исследователей.

Все это вызвало у нас большой интерес и побудило их к более глубокому изучению свойств пирамид, как с математической точки зрения, так и с других точек зрения.

Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.

Легенды и теории

Как предполагают исследователи, наши предки строили пирамиды для других целей, и строили пирамиды по чертежам полученным от внеземного разума. Как считают поклонники теории палеоконтакта, наши предки, возводя чудеса инженерной мысли, получали вдохновение из внеземного источника.

Об этом говорят древние легенды, — которые пришли и от древних майя, от египтян, — с небес спустились боги и повелели им строить пирамиды. Египетский бог Тот, или как его называют “Создатель Вселенной”, — как рассказывают местные легенды, это именно он дал “проект” по созданию комплекса пирамид в Гизе.

Фараон Аменхотеп, при правительстве которого была воздвигнута первая пирамиды, также сказал, что он получил необходимую информацию от богов. Как говорят древние сказания, фараону открылся некий источник информации из неизвестных сфер. После чего и началось строительство великих пирамид.

Сейчас многие исследователи говорят о том, что не могли древние цивилизации, существовавшие на Земле самостоятельно прийти к постройке сооружений в виде пирамид. Как не могли древние культуры, не общавшиеся между собой, разработать единые чертежи по воздвижению пирамид, с практически одинаковыми размерами. С соблюдением всех инженерных требований. Тщательно выдерживая технологию постройки, — настолько тщательно это было разработано и выдержанно, что пирамиды стоят тысячелетия, не поддаваясь разрушению временем.

Как утверждают исследователи, сторонники теории палеоконтакта, между тысячами пирамид расположенными по всей планете существует единая инопланетная связь. Это можно доказать если смотреть на пирамиды с воздуха.

На восходе и закате Солнца, в дни весеннего и осеннего равноденствия, у Великой пирамиды была замечена необыкновенная загадка. Оказывается у нее не 4 стороны, а восемь. И заметить это можно только с высоты, — что и произошло в 1940 году, когда пилот британских ВВС пролетал над комплексом в это время года.

Это говорит о том, что наши предки знали не только об этих днях, и какой эффект они могут проявить на сторонах пирамиды, но говорит о том, что инженеры обладали большими познаниями в математике. И как отмечают специалисты, из этого следует, что Великая пирамида с плато Гиза выделяется из общей массы подобных сооружений. Ее истинная форма может быть замечена только с высоты, и только в определенные дни и время.

Как древние могли создать такую форму, видимую лишь два раза в год в дни равноденствия. По мнению сторонников палеоконтакта, пирамида была построена в центре суши земли. И практически идеально расположена по сторонам света. А шахты, выложенные внутри пирамиды, направлены на созвездия Орион и Сириус.

Ученые считают, что шахты несли функциональное значение – вентиляция пирамиды. Но существует и иное мнение среди ученых. Еще их называют “звездными шахтами”, — через них душа попадает туда, откуда она пришла. И как считали местные жители, через них душа правителя прямиком отправится к созвездию Ориона, где она станет звездой.

— Храм Луны, храм Солнца, храм Кецалькоатля, имеют общий определенный план. На одном из планов комплекса пирамид можно увидеть строение Солнечной системы. А также среди этих комплексов просматривается единая черта, мало того что комплексы похожи между собой — они еще и расположены как звезды в созвездии Ориона, этому же соответствуют и пирамиды Гиза.

Глядя на пирамиды, приходишь к выводу, что у них был общий инженер. Но кто был инженер ? – человек земной культуры ? – или это представитель инопланетных культур. Сейчас исследователи все чаще склоняются к мнению что пирамиды воздвигнуты по указке внеземной культуры. Они служили космическими маяками, и некогда были объединены в единую сеть.

 Пирамида как геометрическое тело

Пирамида - (от греч. pyramis, род. п. pyramidos), многогранник, основание которого многоугольник, а остальные грани треугольники, имеющие общую вершину. По числу сторон основания различают пирамиды треугольные, четырехугольные и т. д.

Общая вершина боковых граней называется вершиной пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Правильная пирамида.

Если основанием пирамиды является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, перпендикулярен плоскости основания, то пирамида называется правильной.

Свойства правильной пирамиды:

1. Всё боковые рёбра правильной пирамиды равны между собой.

2. Все боковые грани являются равными между собой равнобедренными треугольниками.

3. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту боковой грани, которая называется апофемой.

Название “правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке.

Объем пирамиды равен одной трети произведения площади основания на высоту:

Пирамида усечённая - пирамида, которая получается следующим способом: берется произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: подобную исходной пирамиду и многогранник, который называется усеченной пирамидой. Основаниями усеченной пирамиды служат подобные многоугольники.

Если усеченная пирамида получается из правильной пирамиды, то она называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями.

Чертежи сечений пирамиды.

Математические головоломки

Не только внешний вид пирамид, но и их размеры, являются источником многочисленных теорий и гипотез. Если взять периметр пирамиды и разделить ее на высоту, то получится число, равное 2π с точностью до пятнадцати знаков после запятой. Необыкновенное стечение обстоятельств, здесь, скорее, маловероятно. Могли ли древние египтяне знать о существовании числа «пи»?

Архимед в III в. до н. э. определил это число с точностью до двух знаков после запятой, китайский математик в III в н. э. увеличил ее точность в два раза, а в расчетах пирамид эта точность достигает до пятнадцатого знака.

Несмотря на то, что стороны основания пирамиды имеют длину более 200 м, основание имеет форму точно нарисованного квадрата. Каждый угол равен 90°. Разница в длине сторон квадрата ничтожно мала и составляет всего несколько сантиметров.

Астрономические факты

Известно, что если провести горизонтальную линию через центр Земли до пересечения с ее окружностью, потом начертить линии из точек пересечения вверх к центру Луны, а из центра Луны обратно на Землю, то это будут точные пропорции Великой пирамиды.

Египтологи из значений высоты и длины основания Великой пирамиды выводят множество космологических закономерностей и параметров, основными из которых являются:

3,4 — длина витка спирали ДНК для всех живых существ;

3:40 — отношение площадей поверхностей Земли;

1:49 — соотношение объемов Луны и Земли;

1:81,3 — соотношение масс Луны и Земли;

3,14 — число «Пи»;

499 (секунд) — время, за которое солнечный свет проходит расстояние до Земли.

Длина стороны основания, выраженная не в метрах, а в египетских локтях, точно соответствует продолжительности земного года — 365 дней.

О чудесах пирамид сейчас не рассуждают только ленивые: в них практически нет бактерий, говорят, туда поступает космическая энергия и складывается уникальный микроклимат, что связано с формой сооружения. Из научных фактов: в пирамиде существуют места, где биологические продукты сохраняются неограниченное время. Есть в Пирамидах также области, где у человека возникают состояния, стимулирующие его творческую активность, раскрывающие интуицию.

Взглянув на это с точки зрения геометрии, мы можем подойти к пониманию вопроса, описав его очень простым приемом. Согласно теории гармонического резонанса, пирамида является резонатором и генератором, и структура пирамиды может оказывать на человека корректирующее действие. То, что пирамиды правильного сечения благотворно воздействуют на клетки, омолаживая организм и избавляя его от болезней, научный факт, хотя и не имеет объяснения.

По-видимому, по замыслу проектировщиков, Пирамида создавалась как инструмент для воздействия на психофизическую структуру человека. Причем множества людей. Пирамида интересна тем, что в ее конфигурации имеют место не вертикальные плоскости, как в обычной архитектуре, а именно наклонные.

Египетские пирамиды не только древние памятники архитектуры, но и хранилища тайн, закономерностей, научных загадок. Многое в них необъяснимо, но все это интересно современным археологам и историкам.

Золотое сечение (гармоническое деление, деление в крайнем и среднем отношении) – деление отрезка на две части таким образом, что большая его часть является средней пропорциональной между всем отрезком и меньшей его частью.

Строения древней архитектуры приносят человеку чувство гармонии и умиротворения как раз потому, что были созданы по канонам золотого сечения, однако данная зависимость прослеживается не только в средние века, но и в современном мире. Математическую пропорцию можно встретить где угодно: ракушки моллюсков, знаменитые картины художников, даже египетские пирамиды! Золотое сечение вносит в архитектуру, интерьер, картины, и т.д. признаки совершенства, визуально улучшая вид построения.

Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе архитектурных пропорций многих замечательных произведений мирового зодчества, главным образом античности и Возрождения.

Эти слова сказал четыре столетия назад немецкий астроном и математик Иоганн Кеплер, они являются эпиграфом практически ко всем трудам, посвященным «золотому сечению». Гениальный ученый поставил пропорцию «золотого сечения» на один уровень с самой знаменитой геометрической теоремой - теоремой Пифагора

 ИСТОРИЯ ЗОЛОТОГО СЕЧЕНИЯ

«В геометрии существует два сокровища – теорема Пифагора (рисунок 1) и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».

Рисунок 1. Пифагор

В математике принцип «золотого сечения» впервые был сформулирован в «Началах» Эвклида, самом известном математическом сочинении античной науки, написанном в III веке до н.э. Переводчик Дж. Kампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.

В целом все первые геометрические системы – эвклидова геометрия, теорема Пифагора – свидетельствуют о том, насколько волновали древних греков проблемы гармонии, поиск идеальных пропорций и форм. Однако есть предположение, что первыми к принципу золотого сечения пришли все же египтяне. Наиболее известная пирамида Хеопса построена с использованием т.н. золотого треугольника, в котором соотношение гипотенузы к меньшему катету равно золотому сечению. Храмы, барельефы, предметы быта и украшения из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения.

Рисунок 2. Золотое сечение через спираль и треугольник.

 ЗОЛОТОЕ СЕЧЕНИЕ В МАТЕМАТИКЕ

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

Рисунок 3. Храм Парфенона.

Эстетическим каноном древнегреческой культуры этот принцип стал благодаря Пифагору, который изучал в стране пирамид тайные науки египетских жрецов. Их результат воплощен в фасаде древнегреческого храма Парфенона(см. рис. 3), где присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. Также с использованием золотого сечения созданы Афродита Праксителя и театр Диониса в Афинах.

В чем же уникальность этой пропорции? Для начала попробуем разобраться на примере отрезка(см. рис. 4). Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому:

Рисунок 4. Пример золотого сечения на отрезке.

Берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (а + b). Этот правило работает бесконечно, можно делить отрезки сколько угодно долго.

Математически это выглядит так:

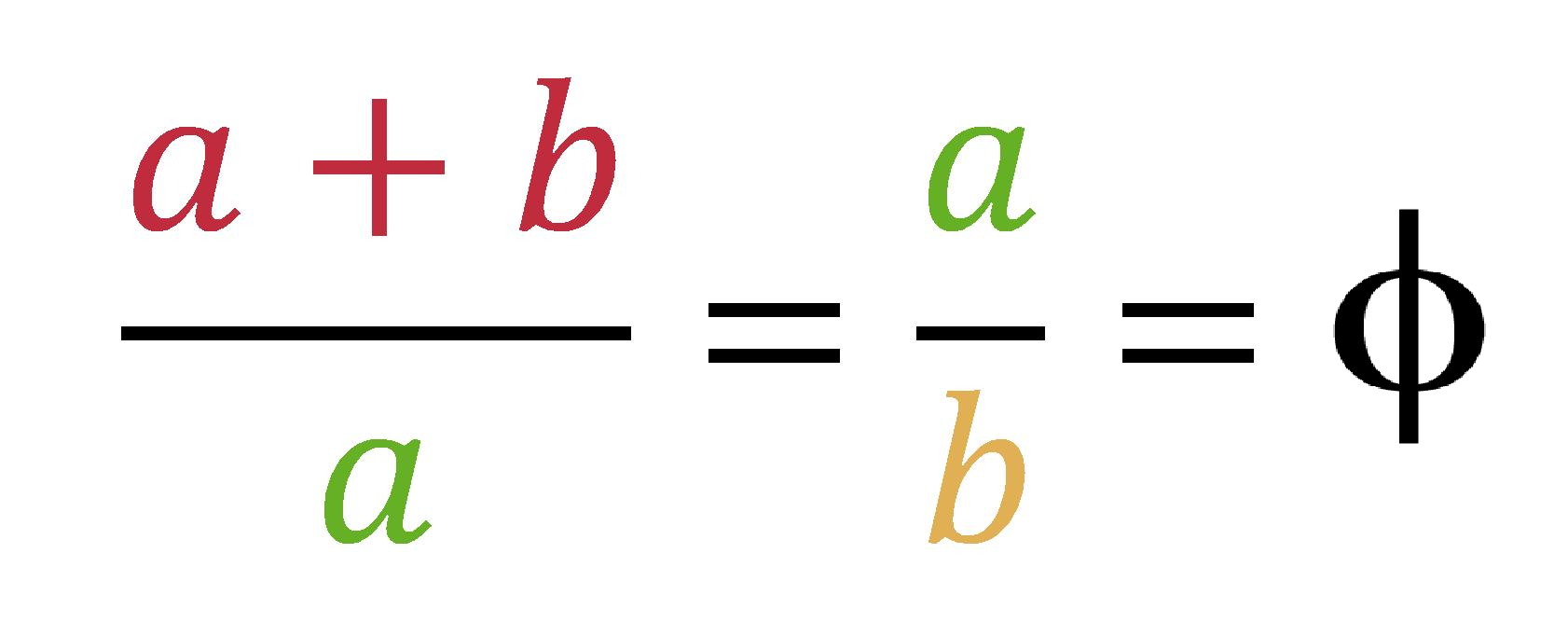
Рисунок 5. Формула пропорции золотого сечения.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62)(см. рис. 6). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Например;

Рисунок 6. Золотой прямоугольник.

МАТЕМАТИЧЕСКИЕ СВОЙСТВА

Однако у золотого сечения существует целый ряд формул, которые не всем дано понять и разобрать, о которых и пойдет речь дальше.

φ — иррациональное алгебраическое число, положительное решение квадратного уравнения  х²- х - 1 = 0, откуда, в частности, следуют соотношения:

• Мера иррациональности равна 2.
• 
  Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон, что и у исходного прямоугольника.
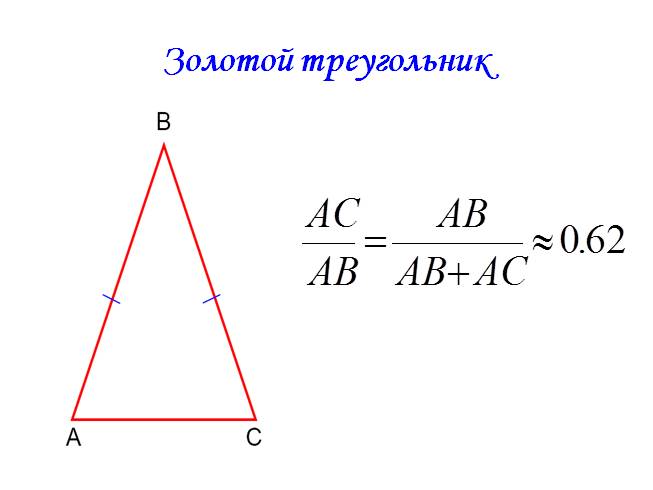
  «Золотой треугольник» – это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1.618.

Есть и «золотой кубоид» (см. рис. 1) – это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Рисунок 1. «Золотой кубоид»

В звездчатом пятиугольнике(см. рис. 2) каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются «золотыми треугольниками». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

Рисунок 2. Звездчатый пятиугольник.

В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, её только скопировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.

«Лотарингский крест», служивший эмблемой «Свободной Франции» (организация, которую в годы второй мировой войны возглавлял генерал де Голль), составлен из тринадцати единичных квадратов. Установлено, что прямая, делящая площадь «лотарингского креста»(см. рис. 3) на две равные части, делит его в золотом отношении.

Рисунок 3. «Лотарингский крест»

Последовательно отсекая от «золотых прямоугольников» квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, можно получить довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали(см. рис. 4). В настоящее время «спираль Архимеда» широко используется в технике. В гидротехнике по «золотой спирали» изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.

Рисунок 4. Спираль

Интерес человека к природе привёл к открытию её физических и математических закономерностей. Красота природных форм рождается во взаимодействии двух физических сил – тяготении и инерции. Золотая пропорция – это математический символ этого взаимодействия, поскольку выражает основные моменты живого роста: стремительный взлёт юных побегов сменяется замедленным ростом «по инерции» до момента цветения.

Рассматривая расположение листьев на общем стебле многих растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте «золотого сечения».

«Золотую спираль» также можно заметить в созданиях природы.

Например, расположение семечек в корзине подсолнечника. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнечника закручено 13 спиралей, в другую – 21. Отношение 13: 21 – отношение Фибоначчи. У более крупных соцветий подсолнечника число соответствующих спиралей больше, но отношение числа спиралей, закручивающихся в разных направлениях также равно числу j.

Природа повторяет свои находки, как в малом, так и в большом. По золотым спиралям закручиваются многие галактики, в частности и галактика Солнечной системы.

Одним из первых проявлений золотого сечения в природе подметил разносторонний наблюдатель, автор многих смелых гипотез немецкий математик и астроном Иоганн Кеплер (1571 – 1630). С ХVII в. наблюдения математических закономерностей в ботанике и зоологии стали быстро накапливаться.

В 1850 г. немецкий учёный А. Цейзинг открыл так называемый закон углов(см. рис. 5), согласно которому средняя величина углового отклонения ветки растения равна примерно 138°. Величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечени

Рисунок 5. Закон углов на примере ветки растения.

ПРИМЕРЫ ЗОЛОТОГО СЕЧЕНИЯ В АРХИТЕКТУРЕ

В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.

Россия также богата постройками по технике золотого сечения. Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.

Рисунок 6. Здание МГУ

В заключении попытаемся сформулировать наиболее популярное и понятное для обывателя определение «золотого сечения».

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Нами был проведен исторический экскурс и разобрана математическая сущность «золотого сечения», рассмотрено строение «золотых фигур».

Знакомство с принципами «золотого сечения», помогает видеть гармонию и целесообразность окружающих нас творений природы и человека. Можно сделать выводы:

во-первых, золотое сечение – это один из основных основополагающих принципов природы;

во-вторых, человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе.

Несмотря на неприятие «золотого сечения» современными «официальными науками», оно повсеместно используется в технике, во многих странах мира, довольно крупные учёные продолжают изучать и искать практическое применение одному из «золотых» математических принципов.

                                          Глава. 1. Биография

Птолемей Клавдий

Рисунок 1. Клавдий Птолемей

С именем Клавдия Птолемея (рисунок 1) связанно множество достижений. Однако о ранних годах его жизни практически ничего не известно. Точной даты рождения и смерти также нет. Его современники никогда не упоминали имя Клавдия Птолемея в своих трудах. Связано это было с тем, что в древности всеми руководило религиозное мировоззрение, и иметь собственное научно обоснованное мнение было практически запрещено. Так как труды Птолемея могли пошатнуть устоявшееся мнение о формировании мира, о нем практически ничего не говорилось. У историков есть мнение, что Птолемей происходил из семьи коронованных особ. Однако эта точка зрения подтверждения не нашла. Из трудов ученого-физика Филиппа Болла известно, что Клавдий долгое время жил в Александрии на территории Египта. Точная дата рождения неизвестна. Также нет данных ни об образовании, ни о семье ученого. Однако его имя - Клавдий - указывает на римское происхождение ученого, а небольшие биографические данные говорят о его связи с Грецией. Поэтому установить точную информацию о его национальной принадлежности не представляется возможным.
 

Труды и достижения

Клавдий Птоломей (Птолемей) (ок.100 – ок.160 гг.) — древнегреческий ученый. Разработал математическую теорию движения планет вокруг неподвижной Земли, позволявшую вычислить их положение на небе. Вместе с теорией движения Солнца и Луны она составила так называемую птолемееву систему мира.

Система Птолемея изложена в его главном труде «Альмагест» — энциклопедии астрономических знаний древних. В «Альмагесте» приведены также сведения по прямолинейной и сферической тригонометрии, впервые дано решение ряда математических задач. В области оптики исследовал преломление и рефракцию света. В труде «География» Клавдий Птолемей дал свод географических сведений античного мира.

  «Алмагест»

  Важнейшим из учено-литературных произведений Клавдия Птоломея было его «Великое собрание» «Алмагест». В этом сочинении, состоящем из 13 книг, содержится все, чем имя автора сделалось знаменитым в астрономии; и все главное из им сделанного в области математики, а именно — тригонометрии. И то, и другое содержится соответственно в 9-ой и 11-ой главах первой книги сочинения, посвященного вообще изложению предварительных астрономических понятий и сведений, между которыми находятся: указание употребительных на небесной сфере кругов и координат и учения — что все звезды имеют сферическое движениe, что Земля есть неподвижный шар, находящийся в центре вселенной; что Солнце, Луна и планеты, кроме общего движения, имеют еще и собственное, направленное противоположно первому, и прочее.

         «Альмагест» является учебником по астрономической теории. Он предназначен для читателей, которые уже изучили логистику, сферику и работы Евклида. С течением веков и изменением мировоззрения современников этот трактат занял основную позицию в древнем научном мире. Уникальность книги обеспечила ей долговечность и почет ученых того времени. Несколько столетий «Альмагест» был образцом сугубо научного подхода к решению разных сложных задач в астрономии. Без этого трактата не развилась бы наука о звездах в средневековой Индии, Персии и Европе.

 
        Упрощение вычисления таблицы хорд (тригонометрия), позволившее Птоломею изложить в одной небольшой главе то, чему его предшественники посвящали обширные сочинения; это достигнуто принятием за основание этого вычисления названной по имени автора теоремы о произведении диагоналей вписанного в круг четырехугольника. К. Птоломей определяет хорды дуг в 11/2° и 3/4° и затем вычисляет по ним приближенно (с точностью до секунд или 3600-х долей) хорду дуги в 1° на основании найденной им теоремы, что отношение большей хорды к меньшей менее отношения стягиваемых ими дуг. Хорда эта оказалась равной 12/60° 5/3600°. В результате он получает таблицу хорд, соответствующих дугам в 0° — 180°, разнящимся между собою на 1/2°. Для определения хорд промежуточных дуг он присоединяет к своей таблице столбец пропорциональных частей, называемых им шестидесятиричными,и допускает в пределах 1/2° существование пропорциональности между изменениями дуг и соответственных хорд.

                      Четверокнижие и другие труды

Ученый разработал «Подручные таблицы» с руководствами, которые исследователи используют и сегодня. В этом уникальном труде он раскрывает научные вопросы астрономии и астрологии. Эта работа позволила открыть дверь в глубины понимания создания Вселенной. «Подручные таблицы» — величайшая книга той эпохи, она состоит из большого количества таблиц, предназначенных для точного определения расположения звезд. Птолемей написал еще множество других работ по астрологии, астрономии, математике, музыке, физике, географии. Они были широко известны в эпоху Средневековья:
 

1. «Фазы неподвижных звезд». Короткий трактат посвящен предсказаниям погоды. В его основе лежит первый метод метеорологии — наблюдение дат и времени синодических явлений планет во Вселенной.
2. «Оптика» — пять книг, где на страницах описана теория о преломлении лучей, зрительных иллюзиях, природе зрения, свойствах

света и зеркальном отражении. Здесь же описаны свойства зеркал.

3. Птолемей разработал таблицу хорд, а также впервые использовал разделение градуса на минуты и секунды.   
4. «Канопская надпись» содержит список различных параметров астрономической системы, нанесенной на каменную плиту, посвященную богам. Исследование этого труда доказало, что он был создан намного раньше, чем популярный «Альмагест».

5. «Четверокнижие» — главный трактат по астрологии Клавдия, ученые его также знают под другим названием на латинском языке — «Квадрипартитум».

6. «Учение о гармонии» — труд Клавдия в трех книгах. К сожалению, до сегодняшнего дня оригинал не дошел. Можно лишь познакомиться с сокращенным вариантом на арабском языке, с которого эту работу затем перевели на латынь.
7. «Планисферий». Небольшая работа автора, раскрывающая на практике гипотезу о стереографической проекции. «География» — описание сведений по античной географии в восьми книгах.
8. «Аналемма» — работа, в которой в доступной форме описаны самые сложные методы астрономических расчетов. 

ГЛАВА 1. ПЕРИОДЫ ЖИЗНИ ЛЕОНАРДО ЭЙЛЕРА

1. 1. Швейцария (1707—1727)

Леонард Эйлер родился в 1707 году в семье Базельского пастора Пауля Эйлера, друга семьи Бернулли. Рано проявил математические способности. Начальную подготовку он проходил дома под руководством своего отца. Пастор готовил своего старшего сына к духовной карьере, но он также изучал математику с ним как развлечение и для развития логического мышления. Одновременно с учебой в гимназии мальчик увлекался математикой, а в последние годы гимназии посещал университетские лекции своего младшего брата Якова.

20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета. Но вскоре способный мальчик привлек внимание профессора Иоганна Бернулли. Ученый давал одаренному студенту математические статьи для изучения, а по субботам приглашал его к себе домой, чтобы вместе анализировать непонятное.

8 июня 1724 года 17-летний Леонард Эйлер произнес речь на латыни о сравнении философских взглядов Декарта и Ньютона и был удостоен степени магистра.

В последующие два года молодой Эйлер написал несколько научных работ. Одна из них, «Диссертация по физике звука», была представлена на конкурс на замещение вакантной должности профессора физики в Базельском университете. Но, несмотря на положительные отзывы, 19-летний Эйлер считался слишком молодым, чтобы быть включенным в список кандидатов на профессорскую должность. Количество научных вакансий в Швейцарии было очень мало, поэтому братья Даниэль и Николай Бернулли уехали в Россию, где создавалась Академия наук.

В начале зимы 1726 года Эйлеру сообщили из Петербурга: по рекомендации братьев Бернулли он был приглашен на должность адъюнкта по физиологии с окладом 200 рублей. Потребовался почти год, чтобы получить аванс на дорожные расходы, и только 5 апреля 1727 года Эйлер навсегда покинул Швейцарию.

1. 2. Первый приезд в Россию (1727—1741)

22 января 1724 года Петр I утвердил проект Санкт-Петербургской Академии. 28 января Сенат издал указ об учреждении Академии. Из 22 профессоров и адъюнктов было 8 математиков, которые также работали в области механики, физики, астрономии, картографии, теории судостроения и службы мер и весов.

Одной из важнейших задач Академии была подготовка домашнего персонала. Позже при Академии были созданы университет и гимназия. В связи с острой нехваткой учебников русского языка Академия попросила своих членов подготовить такое пособие. Эйлер, хотя и был физиологом, составил очень хорошее «руководство по арифметике» на немецком языке, которое было немедленно переведено на русский язык и служило в течение нескольких лет в качестве начального учебника. Это было первое систематическое изложение арифметики на русском языке. К всеобщему удивлению, на следующий год Эйлер свободно говорил по-русски.

В 1730 году интерес к Академии снизился. Некоторые из приглашенных профессоров начали возвращаться домой. Эйлеру предложили вакантную должность профессора физики. Через два года Даниэль Бернулли вернулся в Швейцарию, и Эйлер возглавил его кафедру, став академиком и профессором чистой математики с зарплатой 600 рублей.

В один из последних дней 1733 года 26-летний Леонард Эйлер женился на своей ровеснице Катарине. Молодожены приобрели дом на набережной Невы, где и поселились. В семье Эйлера было 13 детей, но выжили 3 сына и 2 дочери.

Эйлер был феноменально эффективен. По мнению современников, для него жить означало изучать математику. А у молодого профессора было много работы: картография, всевозможные экспертизы, консультации судостроителей и артиллеристов, составление руководств, проектирование пожарных насосов и так далее. они даже требуют от него составления гороскопов, которые Эйлер со всем возможным тактом посылает обычному астроному. Но все это не мешает ему активно проводить собственные исследования.

За время своего первого пребывания в России он написал более 90 крупных научных работ. Значительная часть академических «записок» заполнена работами Эйлера. Он выступал с докладами на научных семинарах, читал публичные лекции, участвовал в выполнении различных технических заказов от государственных ведомств.

В 1735 году перед Академией была поставлена задача выполнить срочный и очень громоздкий астрономический расчет. Группа ученых попросила завершить эту работу в течение трех месяцев, и Эйлер взял на себя обязательство завершить работу за 3 дня — и справился с ней самостоятельно. Однако напряжение не прошло бесследно: он заболел и потерял зрение на правый глаз.

В 1730-х годах Эйлер прославился в Европе. Двухтомная работа «Механика, или наука о движении, в аналитическом изложении», опубликованная в 1736 году, принесла ему мировую известность. В этой монографии Эйлер блестяще применил методы математического анализа для решения задач движения в пустоте и в сопротивляющейся среде. «Те, кто обладает достаточными аналитическими навыками, смогут увидеть все с необычайной легкостью и прочитать всю работу без посторонней помощи», - заключает Эйлер в своем предисловии к книге. С этого момента теоретическая механика становится прикладной частью математики.

«После смерти прославленной императрицы Анны, во время последующего регентства... ситуация начала казаться неопределенной». В самом деле, во время регентства Анны Леопольдовны Петербургская Академия окончательно пришла в упадок. Эйлер думает о возвращении домой. В конце концов он принимает предложение прусского короля Фридриха, который пригласил его в Берлинскую академию на очень выгодных условиях, в качестве директора ее математического отделения. Академия была основана на базе прусского королевского общества, основанного Лейбницем, но в те годы она находилась в удручающем состоянии.

1.3. Пруссия (1741—1766)

29 мая 1741 года было получено разрешение Академии. Эйлер был «освобожден» и утвержден почетным членом Академии. Взамен он обещал оказать всю возможную помощь Петербургской Академии. В течение многих лет молодые российские ученые, которых направляли на стажировки, жили в квартире Эйлера на полном пансионе. Известно об активной переписке Эйлера с Ломоносовым, в трудах которого он высоко ценил "счастливое сочетание теории с экспериментом".

В июне 1741 года Леонард Эйлер с семьей прибыл в Берлин. Он провел там 25 лет и опубликовал около 260 работ.

Поначалу Эйлера тепло встречают в Берлине и даже приглашают на придворные балы. Помимо математики, он занимается практическими задачами, включая лотереи, чеканку монет, прокладку новых водопроводных труб и организацию пенсионных выплат.

В Берлинский период работы Эйлера выходили одна за другой: «введение в анализ бесконечно малых величин»(1748), «морская наука» (1749), "Теория движения Луны"(1753), «инструкции по дифференциальному исчислению». Многочисленные статьи по конкретным вопросам публикуются в изданиях Берлинской и Санкт-Петербургской академий. В 1744 году Эйлер открыл вариационное исчисление.

1765: новый шедевр Эйлера, «Теория движения твердых тел». В 1766 году были опубликованы «элементы вариационного исчисления». Именно здесь впервые появилось название нового раздела математики, созданного Эйлером и Лагранжем.

В 1762 году Екатерина II взошла на российский престол, проводя политику просвещенного абсолютизма. Хорошо осознавая значение науки как для прогресса государства, так и для собственного престижа, она осуществила ряд важных, благоприятных для науки преобразований в системе народного образования и культуры. Императрица предложила Эйлеру руководство математическим классом, звание секретаря конференции Академии и жалованье в 1800 рублей в год. «А если не понравится, - говорилось в письме к ее представителю, - благоволит сообщить свои условия, лишь бы не медлил приездом в Петербург».

Эйлер выдвинул свои условия:

• оклад 3000 рублей в год и должность вице-президента Академии
• ежегодная пенсия в размере 1000 рублей супруги после его смерти
• оплачиваемые должности для трех его сыновей, включая секретаря Академии для старшего.

Эйлер подал прошение королю об отставке со службы, но ответа не получил. Он снова подал заявление — но Фридрих даже не стал обсуждать его отъезд. В ответ Эйлер прекратил работу в Берлинской академии.

Эйлера всячески поддерживали настойчивые ходатайства русского педставительства от имени императрицы. 30 апреля 1766 года Фридрих наконец разрешил великому ученому покинуть Пруссию, после того как он отпустил несколько острых слов. Однако, Кристоф, младший сын Эйлера, служивший подполковником в артиллерии, получил категорический отказ короля покинуть армию. Позже, благодаря заступничеству Екатерины II, он смог присоединиться к своему отцу; в русской армии он дослужился до генерал-лейтенанта.

1.4. Снова Россия (1766—1783)

В июле 1766 года 60-летний Эйлер с семьей прибыл в Санкт-Петербург. Сразу же по прибытии он был принят императрицей. Екатерина II встретила его как августейшего человека и осыпала милостями: выделила 8000 рублей на покупку дома на Васильевском острове и на покупку мебели, предоставила одного из своих поваров на первое время и поручила ему подготовить идеи для реорганизации Академии.

К сожалению, вернувшись в Петербург, Эйлер перестал видеть. Вероятно, именно по этой причине он так и не получил обещанного поста вице-президента Академии. Однако слепота не повлияла на его работоспособность. Эйлер диктовал свою работу мальчику-портному, который все записывал по-немецки. За два с половиной десятилетия работы в России он продиктовал более 400 статей и 10 книг.

1767-1770: работа над двухтомной классической монографией «универсальная арифметика». Это замечательное произведение немедленно публикуется на русском языке. Книга была переведена на многие языки и переиздана около 30 раз. Все последующие учебники алгебры создавались под сильным влиянием книги Эйлера.

В те же годы издаются также три тома «Оптики» и фундаментальное «Интегральное Исчисление» в 3-х томах.

В мае 1771 года в Петербурге произошел крупный пожар, уничтоживший дом и почти все имущество Эйлера. Сам ученый едва спасся. Все рукописи были спасены от пожара; сгорела лишь часть «новой теории движения Луны», но она была быстро восстановлена с помощью самого Эйлера, сохранившего феноменальную память до глубокой старости. Эйлеру пришлось временно переехать в другой дом.

В сентябре того же года по особому приглашению императрицы известный немецкий окулист прибыл в Петербург для лечения Эйлера. После обследования он согласился на операцию и удалил катаракту из левого глаза. Эйлер снова начал видеть. Доктор велел мне беречь глаза от яркого света, не писать, не читать — только постепенно привыкать к новому состоянию. Однако через несколько дней после операции Эйлер снял повязку и вскоре снова потерял зрение. На этот раз все окончательно.

1772: «новая теория движения Луны». Эйлер наконец завершил свою многолетнюю работу, аппроксимировав задачу о трех телах.

В 1773 году по рекомендации Даниэля Бернулли в Петербург из Базеля приехал ученик Бернулли Никлаус Фусс. Это был большое счастье для Эйлера. Фусс обладал редким сочетанием математического таланта и практических навыков, что дало ему возможность приступить к математической работе Эйлера сразу же после его приезда. Фусс вскоре женился на внучке Эйлера. В течение следующих десяти лет, вплоть до своей смерти, Эйлер в основном диктовал ему свои произведения, хотя иногда использовал «глаза своего старшего сына» и других учеников.

1779: издается «универсальная сферическая тригонометрия», первое полное изложение всей системы сферической тригонометрии.

Эйлер работал до последнего. В сентябре 1783 года 76-летний ученый начал испытывать головные боли и слабость. 7 сентября, после обеда с семьей, он внезапно почувствовал себя плохо. Эйлер успел сказать: «Я умираю» - и потерял сознание. Через несколько часов, не приходя в сознание, он умер от кровоизлияния в мозг.

ГЛАВА 2. ВЕЛИКОЕ НАСЛЕДИЕ УЧЕНОГО

Список работ, опубликованных за жизнь Леонарда Эйлера, составлял около пятидесяти страниц. До сих пор сохранилась масса книг, исследований и диссертаций, которые были созданы при жизни Эйлера. Около 700 различных книг, исследований и диссертаций остались в научном наследии великого математика. Петербургская академия опубликовала их в течение 50 лет после смерти Эйлера. Наиболее важные работы Эйлера, которые являются фундаментальными, и это не преувеличение: введение в «Analysin Infinitorum» (1748), «Institutiones Calculus Differentialis» (1755) и «Institutiones Calculi Integralis» (1770). Это трилогия, которая представляет собой сборник математических знаний восемнадцатого века. Она является личным вкладом Эйлера в развитие современной математики.

2.1. Теория чисел

Эйлер продолжил исследования Ферма. Он строго доказал эти гипотезы, значительно обобщил их и объединил в содержательную теорию чисел. Он ввёл в математику исключительно важную «функцию Эйлера» и сформулировал с её помощью «теорему Эйлера». Эйлер создал теорию сравнений и квадратичных вычетов, указав для последних критерий Эйлера.

Он опроверг гипотезу Ферма. Доказал утверждение Ферма о представлении нечётного простого числа в виде суммы двух квадратов.

Дал одно из решений задачи о четырёх кубах.

Ввел дзета-функцию, обобщение которой получило впоследствии имя Римана, где произведение берётся по всем простым числам. Благодаря этому он доказал, что сумма ряда обратных простых расходится.

Эйлер доказал Великую теорему Ферма для n = 3 и n = 4, создал полную теорию непрерывных дробей, исследовал различные классы диофантовых уравнений, теорию разбиений чисел на слагаемые.

В задаче о количестве разбиений натурального числа n получил формулу, выражающую производящую функцию числа разбиений p(n) через бесконечное произведение.

Он открыл, что в теории чисел возможно применение методов математического анализа, положив начало аналитической теории чисел. В основе её лежат тождество Эйлера и общий метод производящих функций.

Эйлер ввёл понятие первообразного корня и выдвинул гипотезу, что для любого простого числа p существует первообразный корень по модулю p; доказать это он не сумел, позднее теорему доказали Лежандр и Гаусс. Большое значение в теории имела другая гипотеза Эйлера — квадратичный закон взаимности, также доказанный Гауссом.

1. 2. Математический анализ

Одна из главных заслуг Эйлера перед наукой — монография «Введение в анализ бесконечно малых» (1748). В 1755 году выходит дополненное «Дифференциальное исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с продуманной терминологией и символикой, откуда многое перешло и в современные учебники. Собственно современные методы дифференцирования и интегрирования были опубликованы в данных трудах.

Основание натуральных логарифмов было известно ещё со времён Непера и Якоба Бернулли, однако Эйлер выполнил настолько глубокое исследование этой важнейшей константы, что с тех пор она носит его имя. Другая исследованная им константа: постоянная Эйлера — Маскерони.

Он делит с Лагранжем честь открытия вариационного исчисления, выписав уравнения Эйлера — Лагранжа для общей вариационной задачи. В 1744 году Эйлер опубликовал первую книгу по вариационному исчислению.

Эйлер значительно продвинул теорию рядов и распространил её на комплексную область, получив при этом знаменитую формулу Эйлера. Большое впечатление на математический мир произвели ряды, впервые просуммированные Эйлером, в том числе не поддававшийся до него никому ряд обратных квадратов:

Современное определение показательной, логарифмической и тригонометрических функций — тоже его заслуга, так же как и их символика и обобщение на комплексный случай. Формулы, часто именуемые в учебниках «условия Коши — Римана», более правильно было бы назвать «условиями Даламбера — Эйлера».

Он первый дал систематическую теорию интегрирования и используемых там технических приёмов, нашёл важные классы интегрируемых дифференциальных уравнений. Он открыл эйлеровы интегралы — ценные классы специальных функций, возникающие при интегрировании: бета-функция и гамма-функция Эйлера. Одновременно с Клеро вывел условия интегрируемости линейных дифференциальных форм от двух или трёх переменных (1739). Первый ввёл двойные интегралы. Получил серьёзные результаты в теории эллиптических функций, в том числе первые теоремы сложения.

С более поздней точки зрения, действия Эйлера с бесконечными рядами не всегда могут считаться корректными, но феноменальная математическая интуиция практически всегда подсказывала ему правильный результат. Впрочем, дело было не только в интуиции, Эйлер действовал здесь достаточно сознательно, во многих важных отношениях его понимание смысла расходящихся рядов и операций с ними превзошло стандартное понимание XIX века и послужило основой современной теории расходящихся рядов, развитой в конце XIX — начале XX века.

Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. С точки зрения математики, XVIII век — это век Эйлера. Если до него достижения в области математики были разрозненны и не всегда согласованны, то Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».

Благодаря Эйлеру в математику вошли общая теория рядов, удивительная по красоте «формула Эйлера», операция сравнения по целому модулю, полная теория непрерывных дробей, аналитический фундамент механики, многочисленные приёмы интегрирования и решения дифференциальных уравнений, число e, обозначение i для мнимой единицы, гамма-функция с её окружением и многое другое.

По существу, именно он создал несколько новых математических дисциплин — теорию чисел, вариационное исчисление, теорию комплексных функций, дифференциальную геометрию поверхностей, специальные функции. Другие области его трудов: диофантов анализ, астрономия, оптика, акустика, статистика и др.  Познания Эйлера были энциклопедичны; кроме математики, он глубоко изучал ботанику, медицину, химию, теорию музыки, множество европейских и древних языков.

Детство

Близ городка Винчи в Италии в селе Акиано, 15 апреля 1452 года родился мальчишка, при переводи на русский его имя звучало так : Леонардо – сын Пьеро из Винчи. Вскоре его имя стало звучать короче и величавее: Леонардо да Винчи, но часто его произносили  просто, как Леонардо.

Уже фамилия Леонардо говорит о том, что его отец был 25-летним  нотариусом, нисколько не стыдился сына, рожденного вне браке, что, впрочем, было типично для Италии.  Первые годы жизни Леонардо жил вместе с матерью, но вскоре отец мальчика женился на богатой и знатной девушке, но этот брак оказался бездетным и Пьеро забрал своего трёхлетнего ребенка на воспитания.  Разлука с матерью поспособствует на то, что художник будет всю жизнь воссоздавать ее образ в своих шедеврах. Некоторое время мальчик жил у деда по отцовской линии — Антонио, а затем отец увёз его в славный город Флоренцию.   В ту пору здесь очень хорошо развивалась промышленность, торговля , банковское дело ,было множество строек новых зданий и храмов, что обеспечивало художников множеством заказов.

Исключительная одаренность будущего великого мастера проявилась очень рано. По словам историка и биографа Вазари, он уже в детстве настолько преуспел в арифметике, что своими вопросами ставил в затруднительное положение преподавателей. Одновременно Леонардо занимался музыкой, прекрасно играл на лире и “божественно пел импровизации”. Однако рисование и лепка больше всего волновали его воображение.

Отец отнес его рисунки своему давнишнему другу, одному из самых разносторонних и известных во Флоренции мастеров - скульптору, ювелиру и живописцу, Андреа Верроккьо. Тот изумился и сказал, что юный Леонардо должен всецело посвятить себя живописи.

Юность

В 1466 году Леонардо поступил в качестве ученика во флорентийскую мастерскую Верроккьо. Именно здесь началось формирование творческой индивидуальности Леонардо да Винчи. Очень скоро ему суждено было превзойти прославленного учителя. Верроккьо часто выполнял работу для Лоренцо Великолепного, правителя Флоренции. После сотен лет рабства и религиозных предрассудков наконец настало время возрождения для изучения наук. Европа оставила Средние века и годы феодализма и много людей переезжало из деревень в города. Благодаря этим изменениям Флоренция, этот замечательный город, заполнился художниками и купцами. Ренессанс достиг и мастерской Верроккьо, в которой рука об руку трудились художники, скульптуры и кузнецы, производившие великолепные механические поделки и музыкальные инструменты и даже ремонтировали всевозможные предметы. Элементарное инженерное искусство являлось составной частью работы художника.

Будучи подмастерьем в мастерской, Леонардо изучал мастерство художника и скульптора и познакомился с широким выбором инструментов для деятельности при поднятии и переноске тяжестей и копании. Позже в своей жизни он будет использовать эти знания как отправную точку для своих многочисленных идей и изобретений. Леонардо занимался всеми видами художественной деятельности, всегда проявляя безграничную любознательность и умение связать искусство с научными познаниями, бывшими результатом пристального наблюдения и неустанного исследования явлений природы.

Геометрия и её связь с природой

Для Леонардо всё в природе связано с землёй, связано между собой и управляется схожими статическими и динамическими принципами, подчиняющимися определённым законам. Он думал, что человек может объяснить естественную философию с помощью видимых свойств рассматриваемого объекта. То, что нельзя увидеть или почувствовать, с точки зрения. Когда Леонардо  пишет о науке, он упоминает не науку в современном понимании этого слова, а интеллектуальный способ видения. В 15 веке наука имела отношение к широкому кругу систематических, интеллектуальных знаний, базирующихся,  в общем и целом на теоретических предположениях. К концу 15 века эти предположения состояли из комбинации, философских концепций, отдельных математических множеств и, иногда, некоторых геометрических форм.

Леонардо считал геометрию ключом к пониманию законов природы. С помощью геометрии Леонардо выстраивал перспективу в живописных работах, делая рисунки механизмов, рассчитывал их массу, необходимую для того, чтобы поднять объект блоками, измерял силу, необходимую для того чтобы метательный снаряд летел под разными углами, и др.

Сложные геометрические задачи Леонардо решал «механически», использую компас и циркуль. Все рисунки Леонардо размечал циркулем. Спустя приблизительно два года после набросков, сделанных в 1493 году,  он чернилами нарисовал вечно движущиеся колеса. И циркули необходимы были ему, чтобы добиться их круглой формы. В конце 15 века тема вечного двигателя была весьма популярна. Никто не мог добиться непрерывного вечного движения с помощью таких колес, но, тем не менее, Леонардо считается их создателем.

Приблизительно в1496 году Леонардо познакомился с Лукой Пачоли, для которого для которого сделал рисунки многогранников. Пачоли опубликовал эти рисунки, включая усеченный звездообразный додекаэдр, в своём трактате «О Божественной пропорции»(1498).

В том же году Леонардо создал уникальную роспись в Сала-делле-Ассе во дворце Сфорца. На сводах и стенах этого зала он изобразил ветви ив, которые затейливо перевязаны декоративными шнурами. Впоследствии часть красочного слоя потускнела и осыпалась, но значительная часть сохранилась и реставрирована.

В этой росписи видно, что Леонардо пытался одновременно добиться эффекта геометрической симметрии природной асимметрии в исполнении деталей.

В последующие годы художник продолжал работать над визуальными решениями геометрических задач, пытаясь решить, например, проблемы квадратуры круга.

Так же как античное искусство повлияло на живопись Леонардо, древние авторы внесли свой вклад его познания в геометрии. При создании геометрических форм он следовал советам Платона; чтобы создать квадратуру круга, он изучал Архимеда; чтобы удвоить размер куба, он использовал решения Эдокса ил Геликона Сизикуса. Сегодня трудно сказать с уверенностью, какие источники были главными для Леонардо, но мы знаем, что он зачастую просил друзей-учёных предоставить ему информацию или какой-либо манускрипт.

В своём творчестве Леонардо усматривал естественную взаимосвязь геометрических законов, пропорций арифметических формул. Изображал ли Леонардо объект, или исследовал его, он знал, что всё это-отображение самой жизни, красоты или безобразия Природы.

Пропорции

Леонардо да Винчи  при создании разных проектов использовал геометрические пропорции. В целом он использовал единицу измерения в одну треть. Извлекая корень из двух в прямоугольнике, он вращал длину диагонали вдоль основания, создавая длинную сторону прямоугольника. В отличие от общепринятого мнения, Леонардо не использовал так называемое «золотое сечение», в котором меньшая длинна пропорциональна большей длине так же, как большая длина пропорциональна сумме большей и меньшей длин.

Ученый и инженер

Леонардо с юности имел склонность к механике и технике. Величайшая его заслуга состоит в том, что он раньше Бэкона теоретически понял значение опытного исследования и раньше Галилея сумел применить экспериментальный метод к самым разнообразным областям знания. Да Винчи был отличный математик, он первый в Италии ввел в употребление знаки "+" и "-".

Так же изобрел особый инструмент для черчения овалов, впервые определил центр тяжести пирамиды.

Изучение геометрии позволило Леонардо впервые создать научную теорию перспективы. "Перспектива, - говорит да Винчи, - есть руль живописи. Она разделяется на три части: 1) укорачивание линий и углов 2) ослабление окраски предметов находящимся между глазом зрителя и предметами слоем воздуха

 3) ослабление контуров".
Он внимательно изучил Архимеда, которого часто цитирует, и старался пойти далее. С замечательной ясностью излагает учёный-художник в общих чертах теорию рычага, поясняя её рисунками; не остановившись на этом, он даёт чертежи, относящиеся к движению тел по наклонной плоскости. Из чертежей ясно, что Леонардо на 80 лет предупредил голландца Стевина и что он уже знал, в каком отношении находится вес двух грузов, находящихся на двух смежных гранях треугольной призмы и соединённых между собой посредством нити, перекинутой через блок.

Леонардо о математике

1. Пусть не читает меня в основаниях моих тот, кто не математик.

 2. Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой.

 3. Удвой квадрат, образуемый диагональным сечением данного куба, и у тебя будет диагональное сечение куба вдвое большего, чем данный: удвой одну из двух квадратных площадей, образуемых при диагональном сечении куба..

4. Механика есть рай математических наук, посредством нее достигают математического плода.

5. Наука инструментальная или механическая - благороднейшая и по сравнению с прочими всеми наиполезнейшая, поскольку при ее посредстве все одушевленные тела, обладающие движением, совершают все свои действия, каковые движения рождаются из центра их тяжести, помещающегося, за исключением неоднородного веса, в середине; и оно имеет бедность и богатство мышц и также рычаг и противорычаг.

6. Пропорция обретается не только в числах и мерах, но также в звуках, тяжестях, временах и положениях и в любой силе, какая бы она ни была.

7. Если источник света xv будет равен источнику света vy, различие между обоими будет такое же, какое между их величинами.

 8. Древние наши пользовались различными приемами, чтобы увидеть, какой путь совершает корабль в каждый час; среди них Витрувий излагает один в своем сочинении об архитектуре - способ, который ошибочен вместе с прочими; и это - мельничное колесо, краев которого касаются морские волны, и посредством полных его обращений начертывается прямая линия, представляющая спрямленную линию окружности этого колеса. Но подобное изобретение имеет применение лишь на ровных и неподвижных поверхностях озер; а если вода движется вместе с кораблем равным движением, тогда такое колесо остается неподвижным, и если движение воды более или менее быстро в сравнении с движением корабля, то и тогда колесо не имеет движения, равного движению корабля, так что подобное изобретение мало имеет цены.

9.Удар, обладая кратчайшей, почти мгновенной жизнью, внезапно производит в противолежащем предмете свое великое и быстрое действие, которое кончено прежде, чем дойдет до основания ударяемого предмета; поэтому обнаружишь ты большее расширение у вершины ударяемого предмета, нежели у основания его.

10. Способ знать качество и густоту воздуха и знать, когда будет дождь.

11. Возможно определить ухом расстояние громового удара при виде молнии по сходству с звуком эхо.

Великий художник

Картины Леонардо получали наполнение жизнью вместе с его познаниями, они были более правдивыми, с людьми, словно можно было заговорить, а в полотно картины войти. Он добивался одухотворенности с сохранением реалистичности, его мнение было в том, что художник должен знать природу и придумывать бесчисленные формы растений и животных. Фантазия для него была следующей ступенью, показывающей мастерство, она позволяла додумать, когда природа уже показала все, что может. Он призывал к развитию воображения и, видя его достижения, ему верили. Леонардо смог коснуться всех областей деятельности.

Его возможности проявлялись в медицинской и анатомической сферах, архитектуре и скульптуре, биологии и механике, картографии, химии, рецептах кулинарии, создании садов, он задумывал развлекательные мероприятия и развлечения. Леонардо хорошо выглядел, о нем говорили, как о высоком, ладно сложенном и привлекательном человеке с хорошей физической силой. Он выделялся острым умом, имел хорошие манеры, красиво говорил, играл на лире и мог очаровать каждого.

Но не все ценили новаторство, были и слова в служении дьяволу, обвинения еретиком. Но так бывает всегда, одаренный мужчина был создан для того, чтобы вести всех вперед, он не считал лучшим обучение по работам других, ценил мудрость как часть опыта. Человека он считал венцом творения, и познавал себя через изучение окружающего. Он объединил философию, художественную сферу, был ученым.

 Мона Лиза

За жизнь художника вышли только около 20 полотен, при этом многие остались не доведенными до конца, что пугало заказчиков. Один из монахов рассказывал о его работе: один день он работал кропотливо и много, а затем мог несколько дней просто всматриваться в рисунок, не делая мазков совсем. Леонардо не разлучался с Моно Лизой до последних дней, работа не большая 77х53 см, но сразу производит впечатление и выглядит монументально. Записей о картине нет, не известна модель, но есть масса догадок, по мнению некоторых образ является собирательным, и просто показывает идеальную даму. Также есть мнение, что художник воссоздал образ матери, или что это переодетый юноша, возможно любовник, ведь картина была завещана ученику. Последний вариант – автопортрет Леонардо, но традиционное мнение – на полотне Лиза Герардини. Она была дочерью купца, точных дат работы нет.

Важно было передать не только лишь внешность, но и суть характера. По мнению Леонардо, это стоит делать жестами, положением тел. Но это не значило, что использовались сложные повороты, вершиной мастерства была глубина при том, что движений почти не было. Особенностью девушки является легкая улыбка, она словно задумчива, вспоминает что-то. Это лицо живое, оно воссоздано настолько одухотворенным, что просто пугает. Ее взгляд осмыслен. Кажется, что она смотрит с полотна. Где бы вы ни стояли, взгляд всегда словно направлен на вас. Немало людей говорят о наличии разницы лица в зависимости от угла обзора.

Дневники

На сегодняшний день от дневников Леонардо уцелело около 7000 страниц, находящихся в разных коллекциях. Сначала бесценные заметки принадлежали любимому ученику мастера, Франческо, но когда тот умер, рукописи исчезли. Отдельные фрагменты начали «всплывать» на рубеже XVIII—XIX вв., немалое число рукописей Леонардо было впервые опубликовано хранителем Амброзианской бибилиотеки . Поначалу они не встретили должного интереса. Многочисленные владельцы даже не подозревали, какое сокровище попало к ним в руки. Но когда учёные установили авторство, выяснилось, что и амбарные книги, и искусствоведческие эссе, и анатомические зарисовки, и странные чертежи, и исследования по геологии, архитектуре, гидравлике, геометрии, боевым фортификациям, философии, оптике, технике рисунка — плод одного человека.

Все записи в дневниках Леонардо сделаны в зеркальном изображении. Леонардо был амбидекстром  - в одинаковой степени хорошо владел правой и левой руками; говорят даже, что он мог одновременно писать разные тексты разными руками. Однако большинство трудов он написал левой рукой справа налево. Многие думают, что таким образом он хотели сделать тайными  свои исследования. Возможно, так оно и есть. По другой версии, зеркальный почерк был его индивидуальной особенностью (есть даже сведения, что ему было проще писать так, чем нормальным образом); существует даже понятие «почерка Леонардо».

Последнии годы

В возрасте 67 лет здоровье Леонардо ухудшилось. Вазари так описывает его последние дни: «В старости он тяжело болел, в течение нескольких месяцев не вставая с постели. Когда он почувствовал близость кончины, он предпринял все усилия для того, чтобы приобщиться к таинствам католической церкви и святой христианской веры: с великими стенаниями он исповедался и покаялся в грехах. И хотя он еле смог подняться, опираясь на плечи друзей и слуг, он был счастлив благочестиво принять святое причастие, стоя на ногах, а не лежа в постели».

Из рассказа Вазари о последних днях Леонардо мы узнаем, что он был соборован католическим священником по всем правилам, причем сам настоял на том, чтобы подняться с постели для принятия Таинства.

В последние дни свой жизни Леонардо раскаивался в том, что оскорбил Господа и все человечество тем, что «не работал в своем искусстве так, как должен был бы». В юности Леонардо верил в Бога как в Высшее Существо, верил в то, что человеческая душа бессмертна. Но он был не только художником, но и ученым, и в своих геологических, астрономических и анатомических исследованиях не мог не задаваться вопросом о существовании человека на Земле, его происхождении и эволюции. И как это часто случается, перед лицом смерти Леонардо примирился с Богом, чтобы подготовить свое отпевание по церковным канонам.

2 мая 1519 года в возрасте 67 лет умер Леонардо до Винчи.

Базари пишет, что перед самой кончиной Леонардо «охватили судороги, посланники смерти». Король в этот момент подошел к нему и приподнял его голову. Через несколько мгновений великий художник скончался на руках у короля. Его смерть вызвала большой резонанс. Вазари сетует: «Утрата Леонардо в высшей степени опечалила каждого, кто его знал, потому что ни один человек, живший доселе, не принес такую славу живописи». Вазари говорит о красоте самого Леонардо, о его способности «выслушать обе стороны», а затем «склонить даже самого упрямого спорщика к противоположной стороне».

Представьте себе мир, в котором все математические операции ведутся римскими цифрами — громоздкими длинными буквенными записями. В этом случае, как и в средние века, нынешняя наука оставалась бы прерогативой очень небольшого круга ученых мужей, поскольку только им были бы подвластны столь замудренные вычисления. Следовательно, никакого развития науки, никакой технической революции, никакого домашнего интернета и никаких полетов в космос. Смартфоны, компьютеры, телевизоры, вся аппаратура, что нас ежедневно окружает, имели бы размеры в несколько комнат, если их вообще получилось бы сконструировать.

Привычные нам с раннего детства арабские цифры (хотя сами арабы их называли индийскими) стали использоваться в Европе не так уж и давно, в масштабах истории — всего лишь с XIII века. Кстати, века до сих пор принято писать римскими цифрами (точнее буквами). Оцените, насколько это непонятно для нас выглядит — XIII вместо 13. Так вот, казалось бы, самый элементарный вид цифр, с позиционной системой записи чисел (это когда левее единиц мы записываем десятки, еще левее сотни и т.д.) получили распространение в Европе всего 700 лет назад. До этого ученые умножали, возводили в степень, решали квадратные и кубические уравнения, тратя только лишь на запись числа уйму времени.

Именно Леонардо Пизанский — 32-летний, никому неизвестный, доморощенный математик — стал проводником арабских цифр в европейскую науку. Позже он стал известен миру под именем Фибоначчи.

ГЕНИАЛЬНЫЙ «БЕЗДЕЛЬНИК»

Родина Фибоначчи — итальянский город Пиза — представлял собой большой оптовый рынок, обнесенный крепостною стеною, и поделенный надвое рекою Арно, со множеством суденышек, доставляющих от городского порта до моря в пяти километрах самый разнообразный товар к большим морским судам, стоящим на рейде. В XII веке родной город Фибоначчи процветал. Пизанских торговцев можно было встретить на всех рынках Средиземноморья, включая Африку. Кроме того, город занимался перевозкой оружия и контингента крестоносцев на Ближний Восток (в том числе Сирию), поэтому расширению его торговых связей благоволил сам Папа Римский.

Конечно, в 1170 году европейские города выглядели мягко говоря совсем не так, как сейчас. Именно в 1170 году в городе Пиза в семье торговца Гильермо Боначчи родился мальчик Леонардо.

К сожалению, нам неизвестно ни единого его прижизненного портрета, поэтому все воздвигнутые памятники, статуи и нарисованные картины являются всего лишь собственной выдумкой их авторов.

Повзрослев, и приобщась к учебе, молодой Леонардо много путешествовал со своим отцом по его торговым делам. Вначале он учился учету товара у торговцев на рынке, позже — математике у учителей Египта и Ближнего Востока. Именно в этот период, зная неудобную систему европейского счета, Леонардо понял насколько проста, понятна и быстра в расчетах восточная система с использованием арабских цифр и записи чисел.

Ну и, судя по всему, он был человеком с юмором, поскольку зачастую в документах подписывался не только официальным «фи Боначчи» («сын Боначчи»), а «Биголло» («бездельник»).

Кропотливый сбор информации и постоянное изучение нового сделали из него самым продвинутым математиком Европы, и сформировали четкий план его наиболее известной книги. В 1200 году он возвращается в родной город, и садится за написание своего основного труда жизни — «Книги Абака».

МОДУС ИНДОРУМ

Это не заклинание Воландеморта и не персонаж компьютерной игры. Звучит зловеще, но знакомо всем чуть ли не с детского сада.

«Модус Индорум» переводится как «метод индейцев» — так Фибоначчи назвал восточный метод счисления, которую он описал в своем самом первом и самом популярном труде — в «Книге Абака». Слово «абак» означает «счет» или «учет».  В этой книге Фибоначчи ввел цифры, которые очень напоминали современные арабские цифры (цитата Фибоначчи из «Книги Абака»):

«Девять индийских фигур: 9 8 7 6 5 4 3 2 1 С этими девятью цифрами и знаком 0, который арабы называют зефиром*, пишется любое число, какое бы то ни было.»  (*«Зефир», точнее по арабски «ас-сифр», что буквально означает «пустой»).

Книга была написана им собственноручно, в 1202 году. Также было создано несколько рукописных копий с нее, поскольку до изобретения книгопечатания оставалось еще 250 лет. До нашего времени дошла только более поздняя редакция рукописи 1227 года, исправленная и дополненная лично самим Фибоначчи, которая сейчас находится в Национальной библиотеке Флоренции.

Труд Фибоначчи был восторженно встречен не только небольшим сообществом придворных математиков, но главным образом торговцами, купцами, простыми людьми, поскольку индуистско-арабская система счисления и понятное и однозначное позиционирование единиц, десятков, сотен и т. д. позволили гораздо упростить все ранее известные математические вычисления.

Римские цифры известны очень давно. Собственно, в Рим посредством этрусков они перекочевали из Греции, примерно в VII в до н.э. До Фибоначчи вся Европа, на которую колоссальное влияние оказала Римская империя и ее система счета, долгие двадцать веков вела все виды учета примерно следующим образом (легко оценить трудоемкость счета, записав, например, простейшее арифметическое выражение «двенадцать в квадрате равно сто сорок четыре»).

Рисунок 1. Система счета, применявшаяся в Римской империи.

А теперь представьте каково вести подобными записями гораздо более сложные вычисления — например, торговые бухгалтерские книги, или рассчитывать провиант для целой армии, или проектировать архитектурное сооружение.

Кроме того, в «Книге Абака» Фибоначчи привел множество примеров применения этой системы счета, изложил их простым и понятным языком, что сразу, как бы сейчас сказали, ушло в массы, в народ.

Труд Фибоначчи был высоко отмечен придворными учеными императора Фридриха II. В то время считалось модным устраивать математические турниры: математики придумывали друг для друга задачки и соревновались в методах их решения. Такие задачи были высланы ими и в адрес Леонардо, который решил их не только успешно, но и очень изящно, просто и понятно, и выслал свои решения их авторам. После этого деятельности Фибоначчи стал покровительствовать сам император.

КРОЛИКИ И УСТРОЙСТВО МИРА

В четвертой главе «Книги Абака» наряду со множеством других примеров вычислений и разнообразных математических задач Фибоначчи описал задачу о размножении пар кроликов. Леонардо старался вывести формулу, точно описывающую последовательность их размножения, которую он подсмотрел у самых обычных живых кроликов (рисунок 2).

С этого момента, последовательность, которая носит теперь название чисел Фибоначчи, будоражит умы ученых всего мира вне зависимости от сферы их деятельности — математиков, биологов, астрономов, архитекторов. Некоторые авторы считают, что в ней заключен вселенский закон развития всего существующего в нашем мире:

Рисунок 2. Последовательность размножения кроликов

Числа Фибоначчи — это числовой ряд, каждое последующее число которого, является суммой двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

Именно этой математической последовательности подчинены все развивающиеся процессы в известной нам Вселенной — направление движения косяка рыб, спирали галактик, в том числе и нашего Млечного пути, форма вихрей тропических ураганов, рост раковин моллюсков, расположение семян на шишках хвойных растений и в соцветиях подсолнечника, расположение ветвей на деревьях и даже строение человеческого тела (рисунок 3).

Рисунок 3. Математическая последовательность, которой подчинены все развивающиеся процессы.

Необходимо отметить, что в своих трудах Фибоначчи просто напомнил миру через восточную систему счисления об этой последовательности, которая была известна задолго до него и египтянам, и древним грекам.

 И, конечно же, огромный интерес к числам Фибоначчи вызван связью этого числового ряда с коэффициентом золотого сечения (φ) — гармонической константой, известной скульпторам, архитекторам, ученым, поэтам, фотографам.

Φ = 1,6180339887498948482 …

Если каждое число последовательности разделить на предыдущее, то результат деления будет стремится к коэффициенту золотого сечения (рисунок 4):

Рисунок 4. 0

Простота и понятность индуистско-арабской системы счисления и последовательность Фибоначчи очевидно показывают насколько математичен окружающий нас мир, в котором все подчинено только лишь законам физики: проявления биологии сводятся в конечном итоге к цепочкам химических реакций, химия которых в свою очередь основана на физике взаимодействия атомов, молекул, электронов. А единственным универсальным языком описания всех этих процессов и зависимостей является математика — своего рода универсальный «компьютерный» язык Вселенной, на котором написаны все формулы мироздания.

НАСЛЕДИЕ

Фибоначчи написал много работ по теории чисел, но практическая необходимость в его простой системе исчисления была так высока среди столь широкого круга простых обывателей и именитых ученых, что она мгновенно разошлась по средневековой Европе. Поэтому остальные его работы отошли на второй план на целых триста лет. И нам они известны из отсылов на них в книгах гораздо более поздних математиков.

Никаких достоверных сведений о жизни, семье и даже могиле Леонардо Фибоначчи до наших дней не дошло. Пизанские экскурсоводы безусловно уверяют, что их великий соотечественник похоронен именно на Монументальном кладбище Пизы (только, к сожалению, никто из них не укажет пальцем, где именно).

Главный талант Леонардо Фибоначчи — простота изложения и, разумеется, практичность. Он прекрасно осознавал необходимость введения новой, простой и удобной системы счета. Ему повезло, его труды были приняты миром, да и не могло быть по-другому. Слишком много людей нуждалось в такой системе исчисления. Точнее сказать все люди. (Для справки, в XIII веке население Европы составляло примерно 120 млн человек, сейчас — 740 млн. И всем этим ста двадцати миллионам так или иначе был нужен нормальный и понятный счет.) А повезло потому, что Церковь могла запросто обвинить его в ереси на каком-нибудь «очень аргументированном» основании и в лучшем случае запретить писать книги. Но, как говорится, удача сопутствует смелым. Кстати, некоторые исследователи переводят фамилию его отца «Боначчи» как «удачливый».

Правильнее назвать Леонардо Фибоначчи — описатель, а правильнее популяризатор. Он ничего не придумал нового, не вывел новых законов математики, не изобрел формулы. Он просто был наблюдательным, остроумным и целесообразным. Он описал все уже известные явления, задачи, вычисления простым и элементарным языком.

Как было написано ранее, сейчас мы живем в мире, который является непосредственным результатом творческой, научной деятельности Леонардо Фибоначчи.

Возможно, если бы не он, спустя время, такой переворот в системе счисления сделал бы кто-то иной, но, как говорится, история не терпит сослагательного наклонения, и поэтому наш современный мир, мир комфорта, мир потребления, мир технического прогресса обязан своим существованием именно ему — Леонардо Фибоначчи.

Ма́уриц Корне́лис Эшер -  нидерландский художник-график. Известен прежде всего своими концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов, яркий представитель имп-арта.

Мауриц родился 17 июня 1898 года в городе Леуварден, в семье инженера. Его родителями были Джордж Арнолд Эшер и Сара Адриана Глейхман-Эшер, Мауриц был их младшим сыном (у него было четыре старших брата, Беренд и Эдмонд от первого брака отца, Арнолд и Ян от второго). Семья жила во дворце «Princessehof», в XVIII веке принадлежавшем Марии Луизе Гессен-Кассельской, матери и регентше статхаудера Вильгельма IV.

В 1903 году семья переехала в Арнем, где с 1907 года мальчик некоторое время учился столярному делу и музыке. С 1912 по 1918 год Мауриц учился в средней школе. Хотя с раннего возраста он проявлял способности к рисованию, его успехи в школе были весьма посредственными (в числе прочего, он провалил экзамен и по рисованию). В 1916 году Эшер выполняет свою первую линогравюру, портрет своего отца Дж. А. Эшера.

В 1917 году семья Эшеров переехала в Остербек. В то время Эшер и его друзья на протяжении нескольких лет увлекались литературой, Мауриц писал стихи и эссе. Он не смог сдать четыре выпускных экзамена и из-за этого не смог получить аттестата зрелости. Несмотря на отсутствие аттестата, из-за ошибки в голландском законодательстве он смог добиться отсрочки от службы в армии для продолжения учёбы и в 1918 году стал брать уроки архитектуры в Техническом училище Делфта. Из-за плохого здоровья Эшер не справился с учёбой и был отчислен, но в 1919 году всё же поступил в Школу архитектуры и декоративных искусств в Харлеме, которую закончил в 1922 году. Там его учителем был художник Самуэль де Мескита, оказавший на молодого человека огромное влияние. Эшер поддерживал дружеские отношения с Мескитой вплоть до 1944 года, когда Мескита 1 февраля был вместе с семьёй арестован и отправлен нацистами в Освенцим. Почти сразу после прибытия Мескита и его жена были умерщвлены в газовой камере.

Эшер совершенно сознательно выбрал карьеру гравёра, а не художника (маслом). По мнению исследователя его творчества Ханса Лохера, Эшера привлекала возможность получения множества оттисков, которую предоставляли графические техники, так как его уже в раннем возрасте интересовала возможность повторения образов.

В 1921 году Эшер с семьёй посетил Северную Италию и Французскую Ривьеру. Он впервые побывал за границей и получил возможность познакомиться с искусством итальянского Возрождения, которое произвело на него сильнейшее впечатление. Он рисует оливковые деревья, начинает эксперименты со сферами, зеркалами. Его гравюры иллюстрируют юмористический буклет его друга, Ада Ван Столка. Первой печатной работой, проданной большим тиражом, была «Святой Франциск» (проповедь птицам). Уже в этой книге начинают появляться мотивы, характерные для позднего творчества Эшера, как, например, искажение пространства в его автопортрете в сферическом зеркале.

В 1921 году Эшер с семьёй посетил Северную Италию и Французскую Ривьеру. Он впервые побывал за границей и получил возможность познакомиться с искусством итальянского Возрождения, которое произвело на него сильнейшее впечатление. Он рисует оливковые деревья, начинает эксперименты со сферами, зеркалами. Его гравюры иллюстрируют юмористический буклет его друга, Ада Ван Столка. Первой печатной работой, проданной большим тиражом, была «Святой Франциск» (проповедь птицам). Уже в этой книге начинают появляться мотивы, характерные для позднего творчества Эшера, как, например, искажение пространства в его автопортрете в сферическом зеркале.

Сразу после переезда в Швейцарию, летом 1935 года, Эшер заезжает по делам в Гаагу, к родителям, где рисует один из известнейших портретов отца. Он пробовал создавать пейзажи, но был разочарован потерей той теплоты, что получалась в пейзажах итальянских. В начале 1936 года он вновь решил отправиться в Южную Европу и предложил одной судоходной компании делать изображения их кораблей и гаваней, в которые те заходят, в обмен на бесплатный проезд. К его удивлению, компания «Адрия» согласилась. Это было последнее большое путешествие художника по средиземноморской Италии. К концу 1936 года Эшер создаёт свою первую картину невозможной реальности «Натюрморт с улицей».

1937 год является переходным в творчестве Эшера, когда он сменил жанр пейзажа на создание произведений, воплощающих геометрические конструкции.

В августе 1937 года семья переезжает в Уккел, пригород Брюсселя. Эшер показывает своему брату-кристаллографу Бееру картину, над которой он работает, и тот видит возможности применения этих идей в кристаллографии. В 1938 году Эшер создаёт основу для своей знаменитой литографии «День и ночь».

14 июня 1939 года в Гааге в возрасте 96 лет умирает Джордж Арнолд Эшер, отец художника. Несколькими месяцами позже Эшер создаёт знаменитые «Метаморфозы». 27 мая 1940 умирает Сара Глейхман Эшер. В это время Брюссель уже был оккупирован нацистской Германией, и Эшер не смог присутствовать на похоронах матери. Вторую половину года он обустраивал её финансовые дела, а также выполнял заказ мэрии Лейдена по украшению здания.

В январе 1941 года Эшеры возвращаются в Нидерланды. С 20 февраля 1941 года семейная пара жила в городе Барн. Ещё до конца войны он выполнил эскиз диплома для Временной академии в Эйндховене. Сразу после войны Эшер участвовал в выставке художников, отказавшихся сотрудничать с нацистским режимом.

В 1946 году Эшер начинает интересоваться технологией глубокой печати, но она отнимала у него слишком много времени, отчего до 1951 года он выполнил не более семи оттисков в манере меццо-тинто, и более не работал в технике углублённой гравюры, предпочитая тоновые контрасты, а не линейный контур.

Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре «Четыре тела»Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос»  В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что, анализируя картину можно догадаться о природе источника света для всей композиции — это окно, которое отражается левой верхней части сферы.

Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.

МОЗАИКА

Регулярное разбиение плоскости, называемое «мозаикой» — это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники. Но Эшер интересовался всеми видами мозаик — регулярными и нерегулярными (прим. перев. нерегулярные мозаики образуют неповоряющиеся узоры) — а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.

Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него «богатейшим источником вдохновения».

Позже в 1957 году в своем эссе о мозаиках Эшер написал:

«В математических работах регулярное разбиение плоскости рассматривается теоретически… Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь, ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.»

Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше. В частности, в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник.) Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех, четырех и шести направленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.

 ФОРМА ПРОСТРАНСТВА

Среди наиболее важных работ Эшера с математической точки зрения являются картины, оперирующие с природой самого пространства. Литография «Три пересекающиеся плоскости» — хороший пример для начала обзора таких картин. Этот пример демонстрирует интерес художника к размерности пространства и способность мозга распознавать трехмерные изображения на двухмерных рисунках. Как будет ниже, Эшер позже использовал данный принцип для создания изумительных визуальных эффектов.

Под влиянием рисунков в книге математика Х. Коксетера Эшер создал много иллюстраций гиперболического пространства. Один из примеров можно увидеть в работе «Предел круга III». Здесь представлен один из двух видов неевклидового пространства, описанных французским математиком Пуанкаре. Чтобы понять особенности этого пространства, представьте, что вы находитесь внутри самой картины. По мере вашего перемещения от центра круга к его границе ваш рост будет уменьшаться также, как уменьшаются рыбы на данной картине. Таким образом путь, который вам надо будет пройти до границы круга будет казаться вам бесконечным. На самом деле, находясь в таком пространстве вы на первый взгляд не заметите ничего необычного в нем по сравнению с обычным евклидовым пространством. Например, чтобы достичь границ евклидового пространства вам также необходимо пройти бесконечный путь. Однако, если внимательно присмотреться, то можно будет заметить некоторые отличия, например, все подобные треугольники имеют в этом пространстве одинаковый размер, и вы не сможете там нарисовать фигуры с четырьмя прямыми углами, соединенными прямыми линиями, так как в этом пространстве не существует квадратов и прямоугольников. Странное место, не правда ли?

 «Предел круга III»